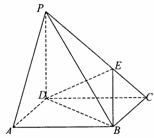
19．(本题满分14分)四棱锥P-ABCD底面是边长为3的正方形，PD⊥平面ABCD，异面直线AD与PB所成角为60°，E为线段PC上一点，PE=2EC.

　 (1)求PD的长；

　 (2)判断PA与平面BDE是否平行，并说明理由；

　 (3)求二面角P-BD-E的大小.

18．(本题满分14分)

　　　　　 某通道有三道门，在前两道门的匣子里各有3把钥匙(第3道门前没有钥匙)，其中一把能打开任何一道门，一把只能打开本道门，还有一把不能打开任何一道门. 现从第一道门开始，随机地从门前的匣子里取一把钥匙开门，若不能进入，就终止；若能进入，再从第二道门的匣子里随机地取一把钥匙，并用已得到的两把钥匙开门，若不能进入，就终止；若能进入，继续用这两把钥匙开第三道门. 记随机变量ξ为打开的门数.

　 (1)求ξ=0时的概率；(2)求ξ的数学期望.

17．已知双曲线的左准线为l，左右焦点分别为F₁，F₂，抛物线C₂的准线为l，焦点为F₂，若C₁与C₂的一个交点为P，则|PF₂|的值为　　　　　 .

16．已知不等式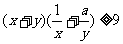对任意正实数x，y恒成立，则正实数a的最小值为　　 .

15．二项式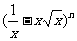的展开式中有含x⁴的项，则n的一个可能值是　　　 .

14．已知α，β是两个不同平面，m，n是两条不同直线，下面四个命题：

　 (1)若α∥β，m⊥β，则m⊥β.　 (2)若m∥n，m⊥α，则n⊥α.

　 (3)若m∥α，m⊥β，则α⊥β.　 (4)若α⊥β，m⊥α，n⊥β，则m⊥n.

　　　 其中正确的命题的序号是　　　 　.

13．已知△ABC的面积为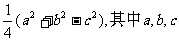分别表示A，B，C所对应的边长，则角C的度数为　　　　 .

12．参数方程所表示的曲线长度为　　　　 .

11．已知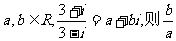的值为　　　　 .

9．有一批种子，每粒发芽的概率为0.6，那么播下9粒种子，发芽数目最大可能为(　　 )

　　　 A．7　　　　　　　　　　　　 B．6　　　　　　　　　　　　 C．5或6　　　　　　　　 D．5

　　　 A．外心　　　　　　　　　 B．内心　　　　　　　　　 C．垂心　　　　　　　　　 D．重心