22．(本小题满分14分)

已知函数(其中a、b、c、d、e∈R)为偶函数，它的图象过点A(0，－1)，且在x=1处的切线方程为2x+y－2=0.

 　(1)求a、b、c、d、e的值，并写出函数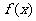的表达式；

　 (2)若对任意x∈R，不等式总成立，求实数t的取值范围.

21．(本小题满分12分)

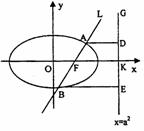
　　　　 如图，已知直线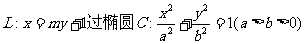的右焦点F，且交椭圆C于A，B两点，点A，F，B在直线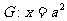上的射影依次为点D，K，E.

　 (1)若抛物线的焦点为椭圆C的上顶点，求椭圆C的方程；

　 (2)对于(1)中的椭圆C，若直线L交y轴于点M，且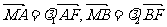，当m变化时，求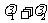的值；

　 (3)连接AE，BD，试探索当m变化时，直线AE、BD是否相交于一定点N？若交于定点N，请求出N点的坐标，并给予证明；否则说明理由.

20．(本小题满分12分)

　　　 已知数列{a_n}中，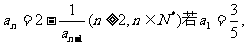

　 (1)数列{b_n}满足，求证：数列{b_n}是等差数列；

　 (2)求数列{a_n}中的最大项和最小项.

19．(本小题满分12分)

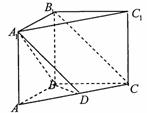
　　　 在直三棱柱ABC-A₁B₁C₁中，AB=BC=BB₁，D为AC的中点，

　 (1)求证：B₁C∥平面A₁BD；

　 (2)若AC₁⊥平面A₁BD，二面角B-A₁C₁-D的余弦值.

18．(本小题满分12分)

　　　　　 有一种舞台灯，外形是正六棱柱ABCDEF-A₁B₁C₁D₁E₁F₁，在其每一个侧面上(不在棱上)安装5只颜色各异的彩灯，假若每只灯正常发光的概率是0.5，若一个面上至少有3只灯发光，则不需要维修，否则需要更换这个面.

　 (1)求面ABB₁A₁需要维修的概率；

　 (2)求最多有两个面需要维修的概率.

17．(本小题满分12分)

　　　 已知函数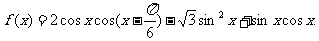

　 (1)求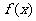的最小正周期；

　 (2)当的值.

16．若m，n均为非负整数，在做m+n的加法时各位均不进位(例如，134+3802=3936)，则称(m，n)为“简单的”有序对，而m+n称为有序数对(m，n)的值，那么值为1942的“简单的”有序对的个数是　　　　　　 .

15．已知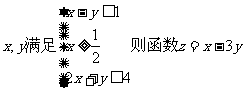的最大值是　　　　　 .

14．若，

　　　 则=　　　　　 .

13．某校有老师200人，男学生1200人，女学生1000人，现用分层抽样的方法从该校所有师生中抽取一个容量为n的样本，已知从女学生中抽取80人，则n=　　　　　　 .