3．已知直线l和两个不同的平面α、β，则下列命题正确的是　　　　　　　　　　　　　　　　　 (　　 )

　 　A．若l∥α，l∥β，则α∥β　　 　　　　　　　 B．若l⊥α，l⊥β，则α∥β

　　C．若l⊥α，α⊥β，，则l∥β　　　 　　　　　　 D．若l∥α，α⊥β，则l⊥β

2．复数在复平面上的对应点位于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　A．第一象限　 　　　　 B．第二象限　　 　　 C．第三象限　　 　　 D．第四象限

1．已知全集U={-1,0，1,2}，集合A={-1，2}，B={ 0,2}，则(C_UA)∩B等于(　　 )

A．{0，1,2}　 　　　　 B．{2}　 　　　　　　　 C．{0}　 　　　　　　　 D．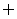

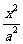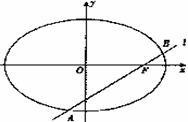
22．(本小题满分14分)已知椭圆+=1(a>b>0)的离心率为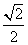，右焦点为F(1，0)，直线l经过点F，且与椭圆交于A、B两点，O为坐标原点．

　 (I)求椭圆的标准方程；

　 (II)若P是椭圆上的一个动点，求|PO|²+|PF|²的最大值和最小值；

　 (III)当直线l绕点F转动时，试问：在x轴上是否存在定点S，使得·为常数?若存在，求出定点S的坐标；若不存在，请说明理由．

21．(本小题满分12分)已知n∈N^*，函数f (x)=x³-nx²+(2ⁿ+1)，x∈R．

　 (I)当n=1时，求f(x)的单调区间；

　 (II)设函数f(x)在[-1，1]上的最大值为a_n，记b_n=，数列{b_n}的前n项和为T_n，求证：T_n<．

20．(本小题满分12分)设p：关于x的不等式x+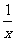≥a²-a对任意的x∈(0，+∞)恒成立；q：关于x的方程x+|x-1|=2a有实数解．若p且q为真，求实数a的取值范围．

19．(本小题满分12分)

如图，PC⊥平面ABC，∠ACB=90°，D为AB中点，AC=BC=PC=2．

　 (I)求证：AB⊥平面PCD；

　 (II)求异面直线PD与BC所成的角的余弦值；

　 (III)求点C到平面PAD的距离．

18．(本小题满分12分)

甲、乙两运动员进行射击训练，已知他们击中的环数都稳定在7，8，9，10环，且每次射击成绩互不影响．射击环数的频率分布条形图如下：

　 (I)求甲运动员击中10环的次数；

　 (II)若将频率视为概率，甲、乙两运动员各自射击两次，求这4次射击中恰有3次击中9环以上 (含9环)的概率.

17．(本小题满分12分)

已知α∈(0，)，且cos2α=.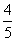

　 (I)求sinα+cosα的值；

　 (II)若β∈(，π)，且5sin(2α+β)=sinβ,求角β的大小 ．

16．为缓解南方部分地区电力用煤紧张的局面，某运输公司提出五种运输方案，据预测，这五种方案均能在规定时间T完成预期的运输任务Q₀，各种方案的运煤总量Q与时间t 的函数关系如下图所示.在这五种方案中，运煤效率(单位时间的运煤量)逐步提高的是_________.(填写所有正确的图象的编号)