2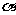．是第四象限角，则所有象限为　　　。

1．＝　　　　。

22．(本小题满分14分)定义F(x，y)= y^x (x>0，y>0)．

(Ⅰ)设函数f(n)= 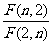　(n∈N*)，求函数f(n)的最小值；

(Ⅱ)解关于x的不等式F(2，x –a -1)≤(a -1)²；

(Ⅲ)设g(x)=F(x,2)，正项数列{a_n}满足：a₁=3，g(a _n+1)= ，求数列{ a_n}

的通项公式，并求所有可能的乘积a_ia_j(1≤i≤j≤n)的和．

21．(本小题满分12分)以F₁(0，-1)，F₂(0，1)为焦点的椭圆C过点P(，1)．

(Ⅰ)求椭圆C的方程；

(Ⅱ)过点S(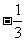，0)的动直线l交椭圆C于A、B两点，试问：在坐标平面上是否存在一个定点T，使得无论l如何转动，以AB为直径的圆恒过点T ? 若存在，求出点T的坐标；若不存在，请说明理由．

20．(本小题满分12分)已知函数f(x)是定义在R上的偶函数，且f(x)的图象关于直线x =2对称．

(Ⅰ)证明：f(x+4)= f(x)；

(Ⅱ)当x∈(4,6)时，f(x)= 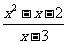．讨论函数f(x)在区间(0，2)上的单调性．

19．(本小题满分12分)如图，PC⊥平面ABC，∠ACB=90°，D为AB中点， AC=BC=PC=2．

(Ⅰ)求证：AB⊥平面PCD；

(Ⅱ)求异面直线PD与BC所成角的大小；

(Ⅲ)设M为线段PA上的点，且AP=4AM，求点A到平面BCM的距离．

18．(本小题满分12分)甲、乙两运动员进行射击训练，已知他们击中的环数都稳定在7，8，9，10环，且每次射击成绩互不影响．射击环数的频率分布条形图如下：

若将频率视为概率，回答下列问题．

　 (Ⅰ)求甲运动员击中10环的概率；

　 (Ⅱ)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率；

　 (Ⅲ)若甲、乙两运动员各自射击1次，ξ表示这2次射击中击中9环以上(含9环)

　 　　　的次数，求ξ的分布列及Eξ．

17．(本小题满分12分)已知α∈(0，)，且cos2α=.

(Ⅰ)求sinα+cosα的值；

(Ⅱ)若β∈(，π)，且5sin(2α+β)=sinβ,求角β的大小 ．

16．为缓解南方部分地区电力用煤紧张的局面，某运输公司提出五种运输方案，据预测，这五种方案均能在规定时间T完成预期的运输任务Q₀，各种方案的运煤总量Q与时间t 的函数关系如下图所示.在这五种方案中，运煤效率(单位时间的运煤量)逐步提高的是_________.(填写所有正确的图象的编号)

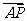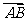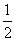
15．P为ΔABC所在平面上的点，且满足=+，则ΔABP与ΔABC的面积之比是_______．