
(1)设集合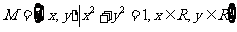 ,
, , 则集合
, 则集合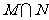 中元素的个数为
中元素的个数为
(A)1 (B)2 (C)3 (D)4
(2)函数 的最小正周期是
的最小正周期是
(A)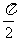 (B)
(B)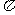 (C)
(C)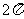 (D)
(D)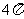
(3)记函数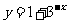 的反函数为
的反函数为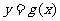 ,则
,则
(A) 2
(B)  (C) 3 (D)
(C) 3 (D) 
(4)等比数列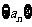 中,
中,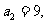
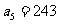 ,则
,则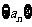 的前4项和为
的前4项和为
(A) 81 (B) 120 (C)168 (D) 192
(5)圆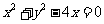 在点
在点 处的切线方程是
处的切线方程是
(A) 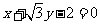 (B)
(B) 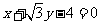
(C) 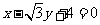 (D)
(D) 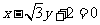
(6)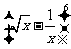 展开式中的常数项为
展开式中的常数项为
(A) 15 (B) 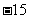 (C)
(C)  20 (D)
20 (D) 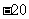
(7) 设复数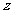 的幅角的主值为
的幅角的主值为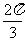 ,虚部为
,虚部为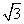 ,则
,则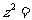
(A) 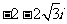 (B)
(B) 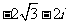
(C) 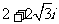 (D)
(D) 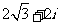
(8) 设双曲线的焦点在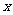 轴上,两条渐近线为
轴上,两条渐近线为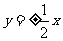 ,则双曲线的离心率
,则双曲线的离心率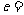
(A) 5 (B) 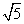 (C)
(C) 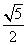 (D)
(D) 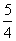
(9)不等式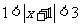 的解集为
的解集为
(A)  (B)
(B) 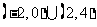
(C) 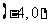 (D)
(D) 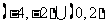
(10)正三棱锥的底面边长为2,侧面均为直角三角形,则此三棱锥的体积为
(A) 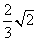 (B)
(B) 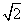 (C)
(C) 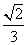 (D)
(D) 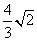
(11)在△ABC中,AB=3,BC= ,AC=4,则边AC上的高为
,AC=4,则边AC上的高为
(A)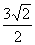 (B)
(B)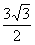 (C)
(C)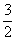 (D)
(D)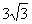
(12)4名教师分配到3所中学任教,每所中学至少1名教师,则不同的分配方案共有
(A) 12 种 (B) 24 种 (C)36 种 (D) 48 种
第Ⅱ卷
(17)(本小题满分12分)
已知等差数列{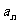 },
},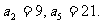
(Ⅰ)求{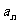 }的通项公式;
}的通项公式;
(Ⅱ)令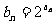 ,求数列
,求数列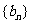 的前n项和Sn.
的前n项和Sn.
(18)(本小题满分12分)
已知锐角三角形ABC中,
(Ⅰ)求证 ;
;
(Ⅱ)设AB=3,求AB边上的高.
(19)(本小题满分12分)
已知8支球队中有3支弱队,以抽签方式将这8支球队分为A、B两组,每组4支.
求:(Ⅰ)A、B两组中有一组恰有两支弱队的概率;
(Ⅱ)A组中至少有两支弱队的概率.
(20)(本小题满分12分)
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB=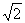 ,侧棱AA1=1,侧面AA1B1B的两条对角线交点为D,B1C1的中点为M.
,侧棱AA1=1,侧面AA1B1B的两条对角线交点为D,B1C1的中点为M.
(Ⅰ)求证CD⊥平面BDM;
(Ⅱ)求面B1BD与面CBD所成二面角的大小.

(21)(本小题满分12分)
若函数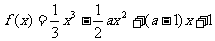 在区间(1,4)内为减函数,在区间(6,+∞)上为增函数,试求实数a的取值范围.
在区间(1,4)内为减函数,在区间(6,+∞)上为增函数,试求实数a的取值范围.
(22)(本小题满分14分)
给定抛物线C: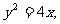 F是C的焦点,过点F的直线
F是C的焦点,过点F的直线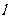 与C相交于A、B两点.
与C相交于A、B两点.
(Ⅰ)设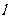 的斜率为1,求
的斜率为1,求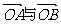 夹角的大小;
夹角的大小;
(Ⅱ)设 ,求
,求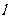 在
在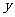 轴上截距的变化范围.
轴上截距的变化范围.
(13)已知a为实数,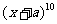 展开式中
展开式中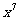 的系数是-15,则
的系数是-15,则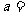 .
.
(14)设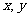 满足约束条件:
满足约束条件:
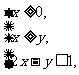
则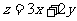 的最大值是
.
的最大值是
.
(15)设中心的原点的椭圆与双曲线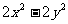 =1有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是
.
=1有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是
.
(16)下面是关于四棱柱的四个命题:
①若有两个侧面垂直于底面,则该四棱柱为直四棱柱
②若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱
③若四个侧面两两全等,则该四棱柱为直四棱柱
④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱
其中,真命题的编号是 (写出所有正确结论的编号).
一项是符合题目要求的.
(1)已知集合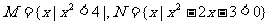 ,则集合
,则集合 =
=
(A){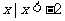 } (B){
} (B){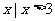 }
}
(C){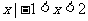 } (D) {
} (D) {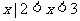 }
}
(2)函数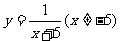 的反函数是
的反函数是
(A)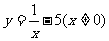 (B)
(B)
(C)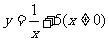 (D)
(D)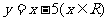
(3)曲线 在点(1,-1)处的切线方程为
在点(1,-1)处的切线方程为
(A)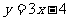 (B)
(B)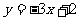 (C)
(C) (D)
(D)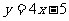
(4)已知圆C与圆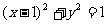 关于直线
关于直线 对称,则圆C的方程为
对称,则圆C的方程为
(A)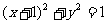 (B)
(B)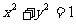
(C)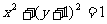 (D)
(D)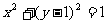
(5)已知函数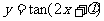 的图像过点
的图像过点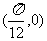 ,则
,则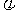 可以是
可以是
(A)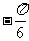 (B)
(B)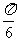 (C)
(C)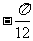 (D)
(D)
(6)正四棱锥的侧棱长与底面边长都是1,则侧棱与底面所成的角为
(A)75° (B)60° (C)45° (D)30°
(7)函数 的图像
的图像
(A)与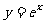 的图像关于
的图像关于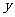 轴对称 (B)与
轴对称 (B)与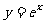 的图像关于坐标原点对称
的图像关于坐标原点对称
(C)与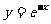 的图像关于
的图像关于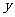 轴对称 (D)与
轴对称 (D)与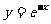 的图像关于坐标原点对称
的图像关于坐标原点对称
(8)已知点A(1,2)、B(3,1),则线段AB的垂直平分线的方程是
(A)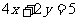 (B)
(B)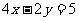 (C)
(C)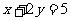 (D)
(D)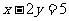
(9)已知向量a、b满足:|a|=1,|b|=2,|a-b|=2,则|a+b|=
(A)1 (B)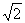 (C)
(C) (D)
(D)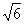
(10)已知球O的半径为1,A、B、C三点都在球面上,且每两点间的球面距离均为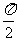 ,则球心O到平面ABC的距离为
,则球心O到平面ABC的距离为
(A)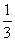 (B)
(B)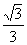 (C)
(C) (D)
(D)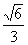
(11)函数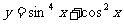 的最小正周期为
的最小正周期为
(A) (B)
(B)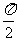 (C)
(C)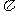 (D)2
(D)2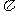
(12)在由数字1,2,3,4,5组成的所有没有重复数字的5位数中,大于23145且小于43521的数共有
(A)56个 (B)57个 (C)58个 (D)60个
第Ⅱ卷
(17)(本小题满分12分)
等差数列{ }的前n项和记为Sn.已知
}的前n项和记为Sn.已知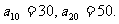
(Ⅰ)求通项 ;
;
(Ⅱ)若Sn=242,求n.
(18)(本小题满分12分)
求函数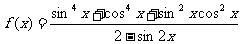 的最小正周期、最大值和最小值.
的最小正周期、最大值和最小值.
(19)(本小题满分12分)
已知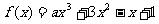 在R上是减函数,求
在R上是减函数,求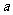 的取值范围.
的取值范围.
(20)(本小题满分12分)
从10位同学(其中6女,4男)中随机选出3位参加测验.每位女同学能通过测验的概率均为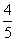 ,每位男同学能通过测验的概率均为
,每位男同学能通过测验的概率均为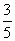 .试求:
.试求:
(I)选出的3位同学中,至少有一位男同学的概率;
(II)10位同学中的女同学甲和男同学乙同时被选中且通过测验的概率.
(21)(本小题满分12分)
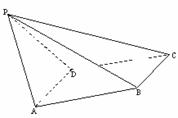
如图,已知四棱锥 P-ABCD,PB⊥AD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120°.
(I)求点P到平面ABCD的距离;
(II)求面APB与面CPB所成二面角的大小.
(22)(本小题满分14分)
设双曲线C: 相交于两个不同的点A、B.
相交于两个不同的点A、B.
(I)求双曲线C的离心率e的取值范围:
(II)设直线l与y轴的交点为P,且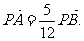 求a的值.
求a的值.
(13)不等式x+x3≥0的解集是 .
(14)已知等比数列{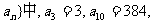 则该数列的通项
则该数列的通项 =
.
=
.
(15)由动点P向圆x2+y2=1引两条切线PA、PB,切点分别为A、B,∠APB=60°,则动点P的轨迹方程为 .
(16)已知a、b为不垂直的异面直线,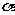 是一个平面,则a、b在
是一个平面,则a、b在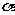 上的射影有可能是 .
上的射影有可能是 .
①两条平行直线 ②两条互相垂直的直线
③同一条直线 ④一条直线及其外一点
在一面结论中,正确结论的编号是 (写出所有正确结论的编号).
(1)设集合U={1,2,3,4,5},A={1,2,3},B={2,5},则A∩( U B)=
(A){2} (B){2,3} (C){3} (D) {1,3}
(2)已知函数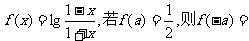
(A)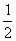 (B)-
(B)-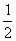 (C)2 (D)-2
(C)2 (D)-2
(3)已知a+b均为单位向量,它们的夹角为60°,那么|a+3b|=
(A)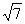 (B)
(B)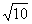 (C)
(C)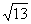 (D)4
(D)4
(4)函数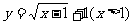 的反函数是
的反函数是
(A) (B)
(B)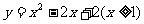
(C)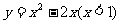 (D)
(D)
(5) 的展开式中常数项是
的展开式中常数项是
(A)14 (B)-14 (C)42 (D)-42
(6)设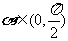 若
若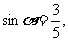 则
则 =
=
(A)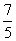 (B)
(B)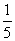 (C)
(C) (D)4
(D)4
(7)椭圆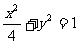 的两个焦点为F1、F2,过F1作垂直于
的两个焦点为F1、F2,过F1作垂直于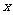 轴的直线与椭圆相交,一个交点为P,则
轴的直线与椭圆相交,一个交点为P,则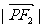 =
=
(A)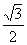 (B)
(B)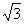 (C)
(C) (D)4
(D)4
(8)设抛物线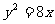 的准线与
的准线与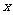 轴交于点Q,若过点Q的直线
轴交于点Q,若过点Q的直线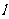 与抛物线有公共点,则直线
与抛物线有公共点,则直线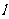 的斜率的取值范围是
的斜率的取值范围是
(A)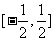 (B)[-2,2] (C)[-1,1] (D)[-4,4]
(B)[-2,2] (C)[-1,1] (D)[-4,4]
(9)为了得到函数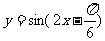 的图象,可以将函数
的图象,可以将函数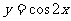 的图象
的图象
(A)向右平移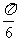 个单位长度 (B)向右平移
个单位长度 (B)向右平移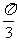 个单位长度
个单位长度
(C)向左平移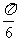 个单位长度 (D)向左平移
个单位长度 (D)向左平移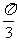 个单位长度
个单位长度
(10)已知正四面体ABCD的表面积为S,其四个面的中心分别为E、F、G、H,设四面体EFGH的表面积为T,则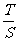 等于
等于
(A)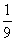 (B)
(B) (C)
(C)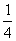 (D)
(D)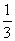
(11)从1,2,……,9这九个数中,随机抽取3个不同的数,则这3个数的和为偶数的概率是
(A)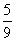 (B)
(B) (C)
(C)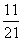 (D)
(D)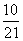
(12)已知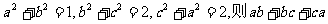 的最小值为
的最小值为
(A)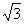 -
-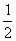 (B)
(B)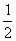 -
-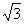 (C)-
(C)-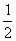 -
-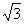 (D)
(D)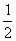 +
+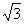
第Ⅱ卷
(17)(本小题满分12分)
已知α为第二象限角,且 sinα=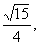 求
求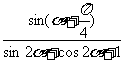 的值.
的值.
(18)(本小题满分12分)
求函数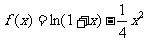 在[0,2]上的最大值和最小值.
在[0,2]上的最大值和最小值.
(19)(本小题满分12分)
某同学参加科普知识竞赛,需回答三个问题.竞赛规则规定:每题回答正确得100分,回答不正确得-100分.假设这名同学每题回答正确的概率均为0.8,且各题回答正确与否相互之间没有影响.
(Ⅰ)求这名同学回答这三个问题的总得分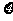 的概率分布和数学期望;
的概率分布和数学期望;
(Ⅱ)求这名同学总得分不为负分(即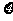 ≥0)的概率.
≥0)的概率.
(20)(本小题满分12分)
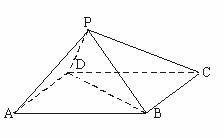
如图,四棱锥P-ABCD中,底面ABCD 为矩形,AB=8,AD=4 ,侧面PAD为等边三角形,并且与底面所成二面角为60°.
,侧面PAD为等边三角形,并且与底面所成二面角为60°.
(Ⅰ)求四棱锥P-ABCD的体积;
(Ⅱ)证明PA⊥BD.
(21)(本小题满分12分)
双曲线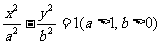 的焦点距为2c,直线
的焦点距为2c,直线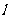 过点(a,0)和(0,b),且点(1,0)到直线
过点(a,0)和(0,b),且点(1,0)到直线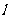 的距离与点(-1,0)到直线
的距离与点(-1,0)到直线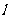 的距离之和
的距离之和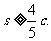 求双曲线的离心率e的 取值范围.
求双曲线的离心率e的 取值范围.
(22)(本小题满分14分)
已知函数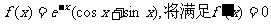 的所有正数
的所有正数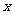 从小到大排成数列
从小到大排成数列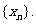
(Ⅰ)证明数列{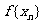 }为等比数列;
}为等比数列;
(Ⅱ)记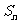 是数列{
是数列{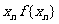 }的前n项和,求
}的前n项和,求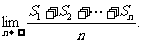
(13)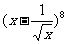 展开式中
展开式中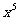 的系数为
.
的系数为
.
(14)向量a、b满足(a-b)·(2a+b)=-4,且|a|=2,|b|=4,则a与b夹角的余弦值等于 .
(15)函数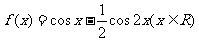 的最大值等于 .
的最大值等于 .
(16)设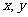 满足约束条件:
满足约束条件:

则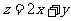 的最大值是
.
的最大值是
.
一项是符合题目要求的.
(1)已知集合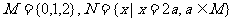 ,则集合
,则集合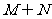 =
=
(A){0} (B){0,1} (C){1,2} (D){0,2}
(2)函数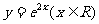 的反函数为
的反函数为
(A)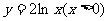 (B)
(B)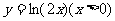
(C)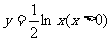 (D)
(D)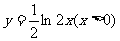
(3)过点(-1,3)且垂直于直线 的直线方程为
的直线方程为
(A)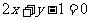 (B)
(B)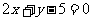
(C) (D)
(D)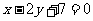
(4)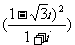 =
=
(A)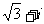 (B)
(B)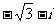 (C)
(C)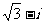 (D)
(D)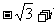
(5)不等式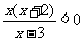 的解集为
的解集为
(A)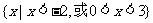 (B)
(B)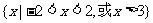
(C)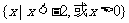 (D)
(D)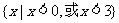
(6)等差数列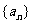 中,
中,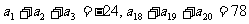 ,则此数列前20项和等于
,则此数列前20项和等于
(A)160 (B)180 (C)200 (D)220
(7)对于直线m、n和平面 ,下面命题中的真命题是
,下面命题中的真命题是
(A)如果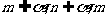 、n是异面直线,那么
、n是异面直线,那么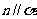
(B)如果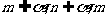 、n是异面直线,那么
、n是异面直线,那么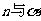 相交
相交
(C)如果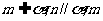 、n共面,那么
、n共面,那么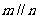
(D)如果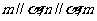 、n共面,那么
、n共面,那么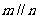
(8)已知椭圆的中心在原点,离心率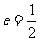 ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线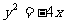 的焦点重合,则此椭圆方程为
的焦点重合,则此椭圆方程为
(A)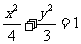 (B)
(B)
(C)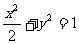 (D)
(D)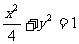
(9)从5位男教师和4位女教师中选出3位教师,派到3个班担任班主任(每班1位班主任),要求这3位班主任中男、女教师都要有,则不同的选派方案共有
(A)210种 (B)420种 (C)630种 (D)840种
(10)已知球的表面积为20π,球面上有A、B、C三点.如果AB=AC=2,BC=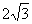 ,则球心到平面ABC的距离为
,则球心到平面ABC的距离为
(A)1 (B)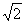 (C)
(C) (D)2
(D)2
(11)△ABC中,a、b、c分别为∠A、∠B、∠C的对边.如果a、b、c成等差数列,
∠B=30°,△ABC的面积为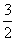 ,那么b=
,那么b=
(A)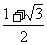 (B)
(B)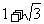 (C)
(C)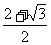 (D)
(D)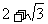
(12)设函数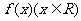 为奇函数,
为奇函数,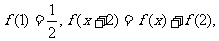 则
则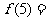
(A)0 (B)1 (C) (D)5
(D)5
第Ⅱ卷
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com