
9.当 时,函数
时,函数 的最小值是
( )
的最小值是
( )
A. 4 B. 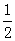 C.2
D.
C.2
D. 
8.若双曲线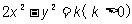 的焦点到它相对应的准线的距离是2,则k= ( )
的焦点到它相对应的准线的距离是2,则k= ( )
A. 6 B. 8 C. 1 D. 4
7.在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是 ( )
A. B.
B. 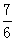 C.
C. 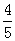 D.
D. 
6.一台X型号自动机床在一小时内不需要工人照看的概率为0.8000,有四台这中型号的自动机床各自独立工作,则在一小时内至多2台机床需要工人照看的概率是 ( )
A.0.1536 B. 0.1808 C. 0.5632 D. 0.9728
5.函数f(x) 是
( )
是
( )
A.周期为 的偶函数 B.周期为
的偶函数 B.周期为 的奇函数
的奇函数
C. 周期为2 的偶函数 D..周期为2
的偶函数 D..周期为2 的奇函数
的奇函数
4.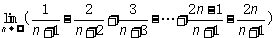 的值为
( )
的值为
( )
A.-1
B.0 C. 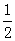 D.1
D.1
3.设函数 在x=2处连续,则a=
( )
在x=2处连续,则a=
( )
A. B.
B. C.
C. D.
D.
2.已知 则
则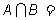 ( )
( )
A. B.
B.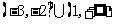
C.  D.
D.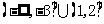
1.已知平面向量 =(3,1),
=(3,1), =(x,-3),且
=(x,-3),且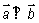 ,则x=
( )
,则x=
( )
A.-3 B.-1 C.1 D.3
22.(本小题满分14分)
设数列 满足
满足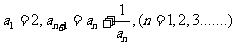
(1)证明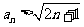 对一切正整数n 成立;
对一切正整数n 成立;
(2)令 ,判断
,判断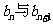 的大小,并说明理由。
的大小,并说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com