
7、函数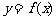 的反函数
的反函数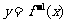 的图像与
的图像与 轴交于点
轴交于点 (如图2所示),则方程
(如图2所示),则方程 在
在 上的根是
上的根是
A.4 B.3 C. 2 D.1
6、已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为
A.5 B.4 C. 3 D. 2
5、给出以下四个命题:
①如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行,
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面
③如果两条直线都平行于一个平面,那么这两条直线互相平行,
④如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.
其中真命题的个数是
A.4 B. 3 C. 2 D. 1
4、已知 是
是 的边
的边 上的中点,则向量
上的中点,则向量
A. B.
B. 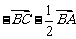 C.
C.  D.
D. 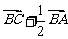
3、下列函数中,在其定义域内既是奇函数又是减函数的是
A. B.
B.  C.
C.  D.
D. 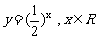
2、若复数 满足方程
满足方程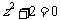 ,则
,则
A.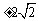 B.
B. 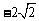 C.
C.
 D.
D.
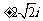
1、函数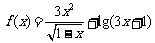 的定义域是
的定义域是
A. B.
B.  C.
C.
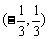 D.
D. 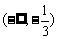
(17)(本小题满分12分)
已知函数 =sin
=sin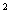 x+
x+ sinx cosx,x∈R
sinx cosx,x∈R
(I)求函数 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(II)函数 的图像可以由函数
的图像可以由函数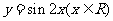 的图像经过怎样的变换得到?
的图像经过怎样的变换得到?
(18)(本小题满分12分)
每次抛掷一枚骰子(六个面上分别标以数字
(I)连续抛掷2次,求向上的数不同的概率;
(II)连续抛掷2次,求向上的数之和为6的概率;
(III)连续抛掷5次,求向上的数为奇数恰好出现3次的概率。
(19)(本小题满分12分)
如图,四面体ABCD中,O、E分别是BD、BC的中点,
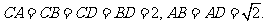
(I)求证: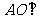 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的大小;
(III)求点E到平面ACD的距离。

(20)(本小题满分12分)
已知椭圆 的左焦点为F,O为坐标原点。
的左焦点为F,O为坐标原点。
(I)求过点O、F,并且与椭圆的左准线 相切的圆的方程;
相切的圆的方程;
(II)设过点F的直线交椭圆于A、B两点,并且线段AB的中点在直线 上,求直线AB的方程。
上,求直线AB的方程。

(21)(本小题满分12分)
已知 是二次函数,不等式
是二次函数,不等式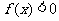 的解集是
的解集是 且
且 在区间
在区间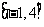 上的最大值是12。
上的最大值是12。
(I)求 的解析式;
的解析式;
(II)是否存在实数 使得方程
使得方程 在区间
在区间 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出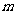 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
(22)(本小题满分14分)
已知数列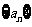 满足
满足
(I)证明:数列 是等比数列;
是等比数列;
(II)求数列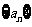 的通项公式;
的通项公式;
(II)若数列 满足
满足 证明
证明 是等差数列。
是等差数列。
(13) 展开式中
展开式中 的系数是
(用数字作答)。
的系数是
(用数字作答)。
(14)已知直线 与抛物线
与抛物线 相切,则
相切,则
(15)已知实数 、
、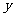 满足
满足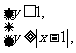 则
则 的最大值是 。
的最大值是 。
(16)已知函数 在区间
在区间 上的最小值是
上的最小值是 ,则
,则 的最小值是 。
的最小值是 。
(1)已知两条直线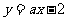 和
和 互相垂直,则
互相垂直,则 等于
等于
(A)2 (B)1 (C)0 (D)
(2)在等差数列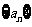 中,已知
中,已知 则
则 等于
等于
(A)40 (B)42 (C)43 (D)45
(3) 是
是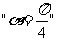 的
的
(A)充分而不必要条件 (B)必要不而充分条件
(C)充要条件 (D)既不充分也不必要条件
(4)已知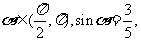 则
则 等于
等于
(A)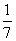 (B)
(B)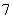 (C)
(C) (D)
(D)
(5)已知集合A={x‖x﹣1︱≤2},B={x︱x2﹣6x﹢8﹤0},则A∩B等于
(A)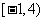 (B)
(B)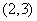 (C)
(C) (D)
(D)
(6)函数 的反函数是
的反函数是
(A) (B)
(B)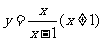
(C) (D)
(D)
(7)已知正方体外接球的体积是 ,那么正方体的棱长等于
,那么正方体的棱长等于
(A) (B)
(B)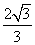 (C)
(C) (D)
(D)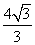
(8)从4名男生和3名女生中选出3人,分别从事三项不同的工作,若这3人中至少有1名女生,则选派方案共有
(A)108种 (B)186种 (C)216种 (D)270种
(9)已知向量 与
与 的夹角为
的夹角为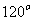 ,
, 则
则 等于
等于
(A)5 (B)4 (C)3 (D)1
(10)对于平面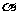 和共面的直线
和共面的直线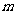 、
、 下列命题中真命题是
下列命题中真命题是
(A)若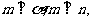 则
则 (B)若
(B)若 则
则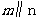
(C)若 则
则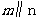 (D)若
(D)若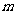 、
、 与
与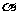 所成的角相等,则
所成的角相等,则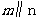
(11)已知双曲线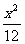 -
-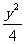 =1的右焦点为F,若过点F的直线与双曲线的右支有且只有一个交点,则此直线斜率的取值范围是
=1的右焦点为F,若过点F的直线与双曲线的右支有且只有一个交点,则此直线斜率的取值范围是
(A)(-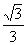 ,
,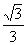 ) (B)(-
) (B)(- ,
, ) (C)[-
) (C)[-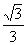 ,
, 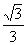 ] (D)[-
] (D)[- ,
, ]
]
(12)已知 是周期为2的奇函数,当
是周期为2的奇函数,当 时,
时, 设
设
 则
则
(A)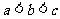 (B)
(B) (C)
(C) (D)
(D)
第二卷
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com