
3.若函数 是定义在R上的偶函数,在
是定义在R上的偶函数,在 上是减函数,且
上是减函数,且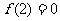 ,则使得
,则使得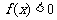 的x的取值范围是 ( )
的x的取值范围是 ( )
A. B.
B.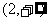 C.
C.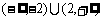 D.(-2,2)
D.(-2,2)
2.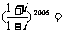 ( )
( )
A. B.-
B.- C.
C. D.-
D.-
1.圆 关于原点(0,0)对称的圆的方程为 ( )
关于原点(0,0)对称的圆的方程为 ( )
A. B.
B.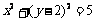
C. D.
D.
20.设点 (
( ,0),
,0),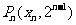 和抛物线
和抛物线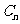 :y=x2+an x+bn(n∈N*),其中an=-2-4n-
:y=x2+an x+bn(n∈N*),其中an=-2-4n- ,
, 由以下方法得到:
由以下方法得到:
x1=1,点P2(x2,2)在抛物线C1:y=x2+a1x+b1上,点A1(x1,0)到P2的距离是A1到C1上点的最短距离,…,点 在抛物线
在抛物线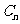 :y=x2+an x+bn上,点
:y=x2+an x+bn上,点 (
( ,0)到
,0)到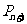 的距离是
的距离是 到
到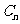 上点的最短距离.
上点的最短距离.
(Ⅰ)求x2及C1的方程.
(Ⅱ)证明{ }是等差数列.
}是等差数列.
19.袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是 ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(Ⅰ) 从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止.(i)求恰好摸5次停止的概率;(ii)记5次之内(含5次)摸到红球的次数为 ,求随机变量
,求随机变量 的分布列及数学期望E
的分布列及数学期望E .
.
(Ⅱ) 若A、B两个袋子中的球数之比为1:2,将A、B中的球装在一起后,从中摸出一个红球的概率是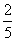 ,求p的值.
,求p的值.
18.如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
(Ⅰ)求证OD∥平面PAB;
(Ⅱ)当k= 时,求直线PA与平面PBC所成角的大小;
时,求直线PA与平面PBC所成角的大小;
(Ⅲ) 当k取何值时,O在平面PBC内的射影恰好为△PBC的重心?

17.如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
(Ⅰ)求椭圆的方程;

(Ⅱ)若直线l1:x=m(|m|>1),P为l1上的动点,使∠F1PF2最大的点P记为Q,求点Q的坐标(用m表示).
16.已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)解不等式g(x)≥f(x)-|x-1|.
15.已知函数f(x)=- sin2x+sinxcosx.
sin2x+sinxcosx.
(Ⅰ) 求f( )的值;
)的值;
(Ⅱ) 设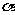 ∈(0,
∈(0, ),f(
),f(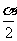 )=
)= -
- ,求sin
,求sin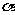 的值.
的值.
14.从集合{O,P,Q,R,S}与{0,1,2,3,4,5,6,7,8,9}中各任取2个元素排成一排(字母和数字均不能重复).每排中字母O、Q和数字0至多只能出现一个的不同排法种数是_________.(用数字作答).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com