
2.tan600°的值是 ( )
A. B.
B.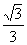 C.
C. D.
D.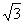
1.设全集U={-2,-1,0,1,2},A={-2,-1,0},B={0,1,2},则(C∪A)∩B=( )
A.{0} B.{-2,-1} C.{1,2} D.{0,1,2}
22.(本小题满分14分)
已知方向向量为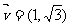 的直线l过点(
的直线l过点( )和椭圆
)和椭圆 的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
(Ⅰ)求椭圆C的方程;(Ⅱ)是否存在过点E(-2,0)的直线m交椭圆C于点M、N,满足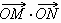 =
= cot∠MON≠0(O为原点).若存在,求直线m的方程;若不存在,请说明理由.
cot∠MON≠0(O为原点).若存在,求直线m的方程;若不存在,请说明理由.
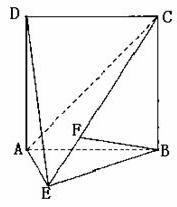
21.(本小题满分12分)
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
(Ⅰ)求证AE⊥平面BCE;
(Ⅱ)求二面角B-AC-E的大小;
(Ⅲ)求点D到平面ACE的距离.
20.(本小题满分12分)
已知函数 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求函数 的单调区间.
的单调区间.
19.(本小题满分12分)
已知{ }是公比为q的等比数列,且
}是公比为q的等比数列,且 成等差数列.
成等差数列.
(Ⅰ)求q的值;
(Ⅱ)设{ }是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
18.(本小题满分12分)
甲、乙两人在罚球线投球命中的概率分别为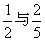 .
.
(Ⅰ)甲、乙两人在罚球线各投球一次,求恰好命中一次的概率;
(Ⅱ)甲、乙两人在罚球线各投球二次,求这四次投球中至少一次命中的概率.
17.(本小题满分12分)
已知 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的值.
的值.
16.把下面不完整的命题补充完整,并使之成为真命题.若函数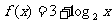 的图象与
的图象与 的图象关于
对称,则函数
的图象关于
对称,则函数 =
.
=
.
(注:填上你认为可以成为真命题的一种情形即可,不必考虑所有可能的情形)
15.非负实数x、y满足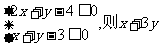 的最大值为
.
的最大值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com