
8.一次二期课改经验交流会打算交流试点学校的论文5篇和非试点学校的论文3篇。若任意排列交流次序,则最先和最后交流的论文都为试点学校的概率是__________(结果用分数表示)
7.在数列 中,
中, ,且对任意大于1的正整数
,且对任意大于1的正整数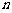 ,点
,点 在直线
在直线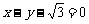 上,则
上,则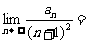 _____________.
_____________.
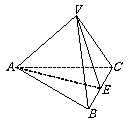
6.如图,在底面边长为2的正三棱锥 中,
中,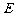 是
是 的中点,若
的中点,若  的面积是
的面积是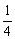 ,则侧棱
,则侧棱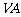 与底面所成角的大小为_____________
(结果用反三角函数值表示).
与底面所成角的大小为_____________
(结果用反三角函数值表示).
5.已知函数 ,则方程
,则方程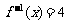 的解
的解 __________.
__________.
4.过抛物线 的焦点
的焦点 作垂直于
作垂直于 轴的直线,交抛物线于
轴的直线,交抛物线于 、
、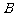 两点,则以
两点,则以 为圆心、
为圆心、  为直径的圆方程是________________.
为直径的圆方程是________________.
3.在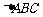 中,
中, 分别是
分别是 、
、 、
、 所对的边。若
所对的边。若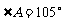 ,
,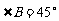 ,
,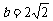 , 则
, 则 __________.
__________.
2.方程 的解
的解 __________.
__________.
1.若复数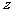 满足
满足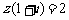 ,则
,则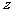 的实部是__________.
的实部是__________.
(17)(本题满分12分)
在ΔABC中,角A、B、C所对的边分别为a、b、c,且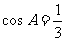 。
。
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,求bc的最大值。
,求bc的最大值。
(18) (本题满分12分)
盒子中有大小相同的球10个,其中标号为1的球3个,标号为2的球4个,标号为5的球3个,第一次从盒子中任取1个球,放回后第二次再任取1个球(假设取到每个球的可能性都相同)。记第一次与第二次取到球的标号之和为ε。
(Ⅰ)求随机变量ε的分布列;
(Ⅱ)求随机变量ε的期望Eε
(19)(本题满分12分)
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= ,AF=1,M是线段EF的中点。
,AF=1,M是线段EF的中点。

(Ⅰ)求证AM∥平面BDE;
(Ⅱ)求二面角A-DF-B的大小;
(20)(本题满分12分)
设曲线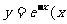 ≥0)在点M(t,c--1)处的切线
≥0)在点M(t,c--1)处的切线 与x轴y轴所围成的三角表面积为S(t)。 (Ⅰ)求切线
与x轴y轴所围成的三角表面积为S(t)。 (Ⅰ)求切线 的方程;
的方程;
(Ⅱ)求S(t)的最大值。

(21)(本题满分12分)已知双曲线的中心在原点,右顶点为A(1,0)点P、Q在双曲线的右支上,支M(m,0)到直线AP的距离为1。
(Ⅰ)若直线AP的斜率为k,且 ,求实数m的取值范围;
,求实数m的取值范围;
(Ⅱ)当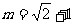 时,ΔAPQ的内心恰好是点M,求此双曲线的方程。
时,ΔAPQ的内心恰好是点M,求此双曲线的方程。
(22)(本题满分14分)
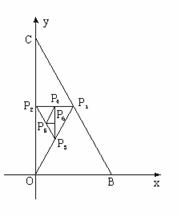
如图,ΔOBC的在个顶点坐标分别为(0,0)、(1,0)、(0,2),设P为线段BC的中点,P2为线段CO的中点,P3为线段OP1的中点,对于每一个正整数n,Pn+3为线段PnPn+1的中点,令Pn的坐标为(xn,yn), 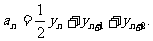
(Ⅰ)求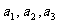 及
及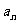 ;
;
(Ⅱ)证明
(Ⅲ)若记 证明
证明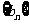 是等比数列.
是等比数列.
(13)已知 则不等式
则不等式 ≤5的解集是
。
≤5的解集是
。
(14)已知平面上三点A、B、C满足 则AB· BC+BC·CA+CA·AB的值等于 。
则AB· BC+BC·CA+CA·AB的值等于 。
(15)设坐标平面内有一个质点从原点出发,沿x轴跳动,每次向正方向或负方向跳1个单位,经过5次跳动质点落在点(3,0)(允许重复过此点)处,则质点不同的运动方法共有 种(用数字作答)。
(16)已知平面α和平面交于直线 ,P是空间一点,PA⊥α,垂足为A,PB⊥β,垂足为B,且PA=1,PB=2,若点A在β内的射影与点B在α内的射影重合,则点P到
,P是空间一点,PA⊥α,垂足为A,PB⊥β,垂足为B,且PA=1,PB=2,若点A在β内的射影与点B在α内的射影重合,则点P到 的距离为
。
的距离为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com