20．(14分) 已知函数f(x)的定义域为{x| x ≠ kπ，k ∈ Z}，且对于定义域内的任何x、y，有f(x­ - y) = 成立，且f(a) = 1(a为正常数)，当0 < x < 2a时，f(x) > 0．

(1) 判断f(x)奇偶性；

(2) 证明f(x)为周期函数；

(3) 求f (x)在[2a，3a] 上的最小值和最大值．

19．(14分) 已知函数．

(1) 若函数f(x)在其定义域内为单调函数，求a的取值范围；

(2) 若函数f(x)的图象在x = 1处的切线的斜率为0，且，已知a₁ = 4，求证：a_n ³ 2n + 2；

(3) 在(2)的条件下，试比较与的大小，并说明你的理由．

18．(14分) 设P(x + a，y₁)，Q(x，y₂)，R(2 + a，y₃)是函数f(x) = 2^x + a 的函数图象上三个不同的点，且满足y₁ + y₃ = 2y₂的实数x有且只有一个，试求实数a的取值范围．

17．(13分) 已知命题p：方程a²x² + ax - 2 = 0在[- 1，1]上有解；命题q：有且只有一个实数x满足不等式x² + 2ax + 2a £ 0．若命题“p或q”是假命题，求a的取值范围．

16．(13分) 某城市在发展过程中，交通状况逐渐受到大家更多的关注，据有关统计数据显示，从上午6点到中午12点，车辆通过该市某一路段的用时y(分钟)与车辆进入该路段的时刻t之间关系可近似地用如下函数给出：．

求从上午6点到中午12点，通过该路段用时最多的时刻．

15．(12分)已知函数．若函数的定义域和值域都是[1，a](a>1)，求a的值．

14．已知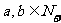，抛物线与x轴有两个不同交点，且两交点到原点的距离均小于1，则的最小值为　　 ．

13．如果函数f(x)的定义域为R，对于m，n Î R，恒有f(m + n) = f(m) + f(n) - 6，且f(- 1)是不大于5的正整数，当x > - 1时，f(x) > 0．那么具有这种性质的函数f(x) = 　　　(注：填上你认为正确的一个函数即可，不必考虑所有可能的情形)

12．如果曲线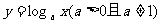与直线y = x相切于点P，则点P的坐标是(e，e)，a =　 　　．

11．已知函数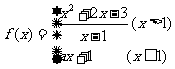连续，则a的值为　　　　　 ．