
(15)(本小题满分13分)
当0<a<1时,解关于x的不等式 .
.
(16)(本小题满分13分)
在△ABC中,a,b,c分别是∠A,∠B,∠C的对边长.已知a,b,c成等比数列,且a2-c2=ac-bc,求∠A的大小及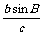 的值.
的值.
(17)(本小题满分15分)
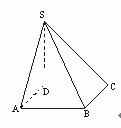
如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD, .
.
(Ⅰ)求证BC⊥SC;
(Ⅱ)求面ASD与面BSC所成二面角的大小;
(Ⅲ)设棱SA的中点为M,求异面直线DM与SB所成角的大小.
(18)(本小题满分15分
已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线y2=2px上,△ABC的重心与此抛物线的焦点F重合(如图).
(Ⅰ)写出该抛物线的方程和焦点F的坐标;
(Ⅱ)求线段BC中点M的坐标;
(Ⅲ)求BC所在直线的方程.

(19)(本小题满分14分)
某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元.该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(Ⅰ)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(Ⅱ)设-次订购量为x个,零件的实际出厂单价为P元,写出函数P=f(x)的表达式;
(Ⅲ)当销售商-次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出-个零件的利润=实际出厂单价-成本)
(20)(本小题满分14分)
下表给出一个“等差数阵”:
|
4 |
7 |
( ) |
( ) |
( ) |
… |
a1j |
… |
|
7 |
12 |
( ) |
( ) |
( ) |
… |
a2j |
… |
|
( ) |
( ) |
( ) |
( ) |
( ) |
… |
a3j |
… |
|
( ) |
( ) |
( ) |
( ) |
( ) |
… |
a4j |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
|
ai1 |
ai2 |
ai3 |
ai4 |
ai5 |
… |
aij |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
其中每行、每列都是等差数列,aij表示位于第i行第j列的数.
(Ⅰ)写出a45的值;
(Ⅱ)写出aij的计算公式;
(Ⅲ)证明:正整数N在该等差数阵中的充要条件是2N+1可以分解成两个不是1的正整数之积.
(11)若f-1(x)为函数f(x)=lg(x+1)的反函数,则f-1(x)的值域是 .
(12) 值为 .
值为 .
(13)据某校环保小组调查,某区垃圾量的年增长率为b,2003年产生的垃圾量为a吨.由此预测,该区下一年的垃圾量为 吨,2008年的垃圾量为 吨.
(14)若直线mx+ny-3=0与圆x2+y2=3没有公共点,则m,n满足的关系式为 ;以(m,n)为点P的坐标,过点P的一条直线与椭圆 的公共点有 个.
的公共点有 个.
(1)在函数y=sin2x,y=sinx,y=cosx,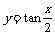 中,最小正周期为的函数是
中,最小正周期为的函数是
(A) y=sin2x (B) y=sinx (C) y=cosx (D) 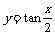
(2)当 时,复数z=(3m-2)+(m-1)i在复平面上对应的点位于
时,复数z=(3m-2)+(m-1)i在复平面上对应的点位于
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
(3)双曲线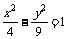 的渐近线方程是
的渐近线方程是
(A) (B)
(B) 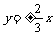
(C)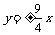 (D)
(D) 
(4)一个圆锥的侧面积是其底面积的2倍,则该圆锥的母线与底面所成的角为
(A) 30° (B)45° (C) 60° (D)75°
(5)在极坐标系中,圆心在( ,)且过极点的圆的方程为
,)且过极点的圆的方程为
(A) (B)
(B)
(C)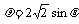 (D)
(D)
(6)已知sin(+)<0,cos(-)>0,则下列不等关系中必定成立的是
(A) (B)
(B)
(C) (D)
(D)
(7)已知三个不等式:ab>0,bc-ad>0, (其中a,b,c,d均为实数).用其中两个不等式作为条件,余下的一个不等式作为结论组成一个命题,可组成的正确命题的个数是
(其中a,b,c,d均为实数).用其中两个不等式作为条件,余下的一个不等式作为结论组成一个命题,可组成的正确命题的个数是
(A)0 (B)1 (C)2 (D)3
(8)两个完全相同的长方体的长、宽、高分别为5cm,4cm,3cm,把它们重叠在一起组成一个新长方体.在这些新长方体中,最长的对角线的长度是
(A) cm (B)
cm (B) cm (C)
cm (C) cm (D)
cm (D) cm
cm
(9)在100件产品中有6件次品.现从中任取3件产品,至少有1件次品的不同取法的种数是
(A)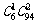 (B)
(B)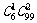 (C)
(C) (D)
(D)
(10)期中考试以后,班长算出了全班40个人数学成绩的平均分为M.如果把M当成一个同学的分数,与原来的40个分数一起,算出这41个分数的平均值为N,那么M∶N为
(A) (B)1 (C)
(B)1 (C) (D)2
(D)2
第Ⅱ卷
(17)(本小题满分12分)
已知正四棱柱ABCD-A1B1C1D1,AB=1,AA1=2,点E为CC1中点,点F为BD1中点.
(Ⅰ)证明EF为BD1与CC1的公垂线;
(Ⅱ)求点D1到BDE面的距离.
(18)(本小题满分12分)
已知抛物线C1:y=x2+2x和C2:y=-x2+a.如果直线l同时是C1和C2的切线,称l是C1和C2的公切线,公切线上两个切点之间的线段,称为公切线段.
(Ⅰ)a取什么值时,C1和C2有且仅有一条公切线?写出此公切线的方程;
(Ⅱ)若C1和C2有两条公切线,证明相应的两条公切线段互相平分.
(19)(本小题满分12分)
已知数列 |足
|足 
(I)求 ;
;
(II)证明
(20)(本小题满分12分)
有三种产品,合格率分别是0.90,0.95和0.95,各抽取一件进行检验.
(I)求恰有一件不合格的概率;
(II)求至少有两件不合格的概率.
(精确到0.001)
(21)(本小题满分12分)
已知函数f(x)=sin( x+)( >0,0≤≤)是R上的偶函数,其图象关于点 对称,且在区间
对称,且在区间 上是单调函数,求 和 的值.
上是单调函数,求 和 的值.
(22)(本小题满分12分)
已知常数a>0,向量c = (0,a),i=(1,0).经过原点O以c+ i为方向向量的直线与经过定点A(0,a)以i-2c为方向向量的直线相交于点P,其中∈R.试问:是否存在两个定点E、F,使得| PE | + | PF |为定值.若存在,求出E、F的坐标;若不存在,说明理由.
(13) 展开式中x9的系数是
.
展开式中x9的系数是
.
(14)某公司生产三种型号的轿车,产量分别为1200辆,6000辆和2000辆,为检验该公司的产品质量,现用分层抽样的方法抽取46辆进行检验,这三种型号的轿车依次应抽取_______,_______,_________辆.
(15)在平面几何里,有勾股定理:“设△ABC的两边AB,AC互相垂直,则 AB2+AC2=BC2.”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积间的关系,可以得出的正确结论是:“设三棱锥A-BCD的三个侧面ABC、ACD、ADB两两相互垂直,则 ”.
(16)将3种作物种植在如图5块试验田里,每块种植一种作物且相邻的试验田不能种植同一作物,不同的种植方法共有__________________种.(以数字作答)

(1)不等式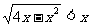 的解集是
的解集是
(A)(0,2) (B)(2,+∞)
(C)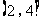 (D)(-∞,0)
(D)(-∞,0) (2,+∞)
(2,+∞)
(2)抛物线y=ax2的准线方程是y=2,则a的值为
(A)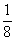 (B)
(B) (C)8 (D)-8
(C)8 (D)-8
(3)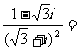
(A) (B)
(B)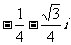
(C)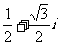 (D)
(D)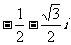
(4)已知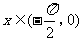 ,
, ,则tan 2x=
,则tan 2x=
(A)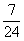 (B)
(B)
(C) (D)
(D)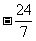
(5)等差数列| an |中,已知 ,则n为
,则n为
(A)48 (B)49 (C)50 (D)51
(6)双曲线虚轴的一个端点为M,两个焦点为F1,F2,∠F1M F2=120°,则双曲线的离心率为
(A) (B)
(B) (C)
(C) (D)
(D)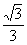
(7)设函数 若f(x0)>1,则x0的取值范围是
若f(x0)>1,则x0的取值范围是
(A)(-1,1) (B)(-1,+∞)
(C)(-∞,-2) (0,+∞) (D)(-∞,-1)
(0,+∞) (D)(-∞,-1) (1,+∞)
(1,+∞)
(8)O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足 ,
,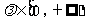 ,则P的轨迹一定通过△ABC的
,则P的轨迹一定通过△ABC的
(A)外心 (B)内心
(C)重心 (D)垂心
(9)函数 ,x∈(1,+∞)的反函数为
,x∈(1,+∞)的反函数为
(A) ,x∈(1,+∞) (B)
,x∈(1,+∞) (B) ,x∈(0,+∞)
,x∈(0,+∞)
(C) ,x∈(-∞,0) (D)
,x∈(-∞,0) (D) ,x∈(-∞,0)
,x∈(-∞,0)
(10)棱长为a的正方体中,连结相邻面的中心,以这些线段为棱的八面体的体积为
(A)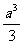 (B)
(B) (C)
(C) (D)
(D)
(11)已知长方形的四个顶点A(0,0),B(2,0),C(2,1)和D(0,1),一质点从AB的中点P0沿与AB夹角为 的方向射到BC上的点P1后,依次反射到CD、DA和AB上的点P2、P3和P4(入射角等于反射角).设P4与P0重合,则tan =
(A) (B)
(B) (C)
(C) (D)1
(D)1
(12)一个四面体的所有棱长都为 ,四个顶点在同一球面上,则此球的表面积为
,四个顶点在同一球面上,则此球的表面积为
(A)3 (B)4 (C) (D)6
(D)6
第Ⅱ卷
(17)(本题满分12分)
已知复数z1=cos-i,z2=sin+i,求|z1·z2|的最大值和最小值.
(18)(本题满分12分)

已知平行六面体ABCD-A1B1C1D1中,A1A⊥平面ABCD,AB=4,AD=2.若B1D⊥BC,直线B1D与平面ABCD所成的角等于30°,求平行六面体ABCD-A1B1C1D1的体积.
(19)(本题满分14分)
已知函数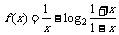 ,求函数f(x)的定义域,并讨论它的奇偶性和单调性.
,求函数f(x)的定义域,并讨论它的奇偶性和单调性.
(20)(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.

如图,某隧道设计为以双向四车道,车道总宽22米,要求通行车辆限高4.5米,隧道全长2.5千米,隧道的拱线近似地看成半个随圆的形状.
(1)若最大拱高h为6米,则隧道设计的拱宽l是多少?
(2)若最大拱高h不小于6米,则应如何设计拱高h和拱宽l,才能使半个椭圆形隧道的土方工程量最小?
(半个椭圆的面积公式为 ,柱体体积为:底面积乘以高,本题结果均精确到0.1米)
,柱体体积为:底面积乘以高,本题结果均精确到0.1米)
(21)(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分5分,第3小题满分7分.
在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点,已知|AB|=2|OA|,且点B的纵坐标大于零.
(1)求向量 的坐标;
的坐标;
(2)求圆x2-6x+y2+2y=0关于直线OB对称的圆的方程;
(3)是否存在实数a,使抛物线y=ax2-1上总有关于直线OB对称的两个点?若不存在,说明理由;若存在,求a的取值范围.
(22)(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分8分,第3小题满分6分.
已知数列{an}(n为正整数)是首项为a1,公比为q的等比数列.
(1)求和:
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明;
(3)设q≠1,Sn是等比数列{an}的前n项和,求:

|
符号意义 |
本试卷所有符号 |
等同于《实验教材》符号 |
|
正切、余切 |
tg、ctg |
tan、cot |
(13)下列函数中,既为偶函数又在(0,)上单调递增的是
(A)y=tg|x|. (B)y=cos(-x).
(C)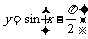 (D)
(D)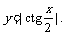
(14)在下列条件中,可判断平面与平行的是
(A)、都垂直于平面.
(B)内存在不共线的三点到的距离相等.
(C)l,m是内两条直线,且l∥, m∥.
(D)是两条异面直线,且l∥, m∥, l∥, m∥.
(15)在P(1,1)、Q(1,2)、M(2,3)和 四点中,函数y=ax的图象与其反函数的图象的公共点只可能是点
四点中,函数y=ax的图象与其反函数的图象的公共点只可能是点
(A)P. (B)Q. (C)M. (D)N.
(16)f(x)是定义在区间[-c,c]上的奇函数,其图象如图所示.令g(x)=af(x)+b,则下列关于函数g(x)的叙述正确的是
(A)若a<0,则函数g(x)的图象关于原点对称.
(B)若a=1,0<b<2,则方程g(x)=0有大于2的实根.
(C)若a=-2,b=0,则函数g(x)的图象关于y轴对称.
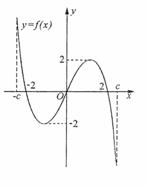
(D)若a≠1, b=2,则方程g(x)=0有三个实根.
(1)函数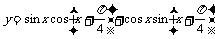 的最小正周期T=
.
的最小正周期T=
.
(2)若 是方程2cos(x+)=1的解,其中∈(0,2),则=
.
是方程2cos(x+)=1的解,其中∈(0,2),则=
.
(3)在等差数列{an}中,a5=3,a6=-2,则a4+a5+…+a10= .
(4)已知定点A(0,1),点B在直线x+y=0上运动,当线段AB最短时,点B的坐标是
.
(5)在正四棱锥P-ABCD中,若侧面与底面所成二面角的大小为60°,则异面直线PA与BC所成的大小等于 .(结果用反三角函数值表示)
(6)设集合A={x| |x|<4},B={x| x2-4x+3<4},则集合{x| x∈A且x A∩B }= .
(7)在△ABC中,sinA:sinB:sinC=2:3:4,则∠ABC= .(结果用反三解函数值表示)
(8)若首项为a1,公比为q的等比数列{an}的前n项和总小于这个数列的各项和,则首项a1,公比q的一组取值可以是(a1,q)= .
(9)某国际科研合作项目成员由11个美国人、4个法国人和5个中国人组成。现从中随机选出两位作为成果发布人,则此两人不属于同一个国家的概率为 .(结果用分数表示)
(10)方程x3+lgx=18的根x≈ .(结果精确到0.1)
(11)已知点 ,
, ,
, ,其中n为正整数.设Sn表示△ABC外接圆的面积,则
,其中n为正整数.设Sn表示△ABC外接圆的面积,则 =
.
=
.
(12)给出问题:是F1、F2双曲线 的焦点,点P在双曲线上.若点P到焦点F1的距离等于9,求点P到焦点的F2距离.某学生的解答如下:双曲线的实轴上为8,由||PF1|-| PF2||=8,即|9-| PF2||=8,得| PF2|=1或17.
的焦点,点P在双曲线上.若点P到焦点F1的距离等于9,求点P到焦点的F2距离.某学生的解答如下:双曲线的实轴上为8,由||PF1|-| PF2||=8,即|9-| PF2||=8,得| PF2|=1或17.
该学生的解答是否正确?若正确,请将他的解题依据填在下面空格内;或不正确,将正确结果填在下面空格内.
.
22.(本小题满分14分)已知 ,且
,且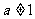 ,数列
,数列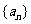 的前
的前 项和为
项和为 ,它满足条件
,它满足条件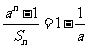 .数列
.数列
中, ·
·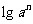 .
.
(1)求数列 的前
的前 项和
项和 ;
;
(2)若对一切 都有
都有 ,求
,求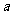 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com