(1)设全集I={1,2,3,4,5,6,7},集合A={1,3,5,7},B={3,5}.则

(2)当a>1时,在同一坐标系中.函数y=a^-x与y=log_ax的图象是

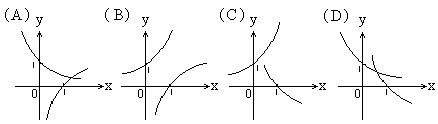
(3)若sin²x>cos²x,则x的取值范围是

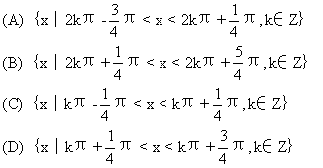
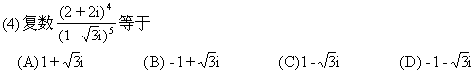
(5)6名同学排成一排,其中甲、乙两人必须排在一起的不同排法有

(A)720种　　 (B)360种　 (C)240种　 (D)120种

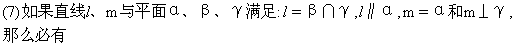
(A)α⊥γ且l⊥m　　　　　　　 (B)α⊥γ且m∥β

(C)m∥β且l⊥m　　　　　　　　 (D)α∥β且α⊥γ

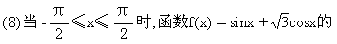
(C)最大值是2,最小值是-2　　　 (D)最大值是2,最小值是-1

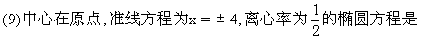
(10)圆锥母线长为1,侧面展开图圆心角为240°,该圆锥的体积是

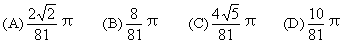
(11)椭圆25x²-150x+9y²+18y+9=0的两个焦点坐标是

(A)(-3,5),(-3,-3)　　 　　　　(B)(3,3),(3,-5)

(C)(1,1),(-7,1)　　　　　　　 (D)(7,-1),(-1,-1)

(12)将边长为a的正方形ABCD沿对角线AC折起,使得BD=a,则三棱锥D-ABC的体积为

(13)等差数列{a_n}的前m项和为30,前2m项和为100,则它的前3m项和为

(A)130　　　　　　　　　　　　 (B)170

(C)210　　　　　　　　　　　　 (D)260

(15)设f(x)是(-∞,+∞)上的奇函数,f(x+2)=f(x),当0≤x≤1时,f(x)=x,则f(7,5)等于

(A)0.5　　　　　　　　　　　　 (B)-0.5

(C)1.5　　　　　　　　　　　　 (D)-1.5

　第Ⅱ卷

(20)(本小题满分11分)

(21)(本小题满分12分)

(22)(本小题满分12分)

如图,在正三棱柱ABC-A₁B₁C₁中,E∈BB_1，截面A₁EC⊥侧面AC₁.

(Ⅰ)求证:BE=EB₁;

(Ⅱ)若AA₁=A₁B₁;求平面A₁EC与平面A₁B₁C₁所成二面角(锐角)的度数.

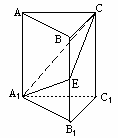
注意:在下面横线上填写适当内容,使之成为(Ⅰ)的完整证明,并解答(Ⅱ).

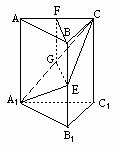
(Ⅰ)证明:在截面A₁EC内,过E作EG⊥A₁C,G是垂足.

① ∵　　　　　　　　　　　　　　　　　　　

　∴EG⊥侧面AC₁;取AC的中点F,连结BF,FG,由AB=BC得BF⊥AC,

② ∵　　　　　　　　　　　　　　

　∴BF⊥侧面AC₁;得BF∥EG,BF、EG确定一个平面,交侧面AC₁于FG.

③ ∵　　　　　　　　　　　

　∴BE∥FG,四边形BEGF是平行四边形,BE=FG,

④ ∵　　　 　　　　　　　　　　　　

　∴FG∥AA₁,△AA₁C∽△FGC,

⑤ ∵　　　　　　　　　　

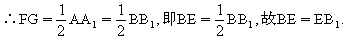
(23)(本小题满分10分)

某地现有耕地10000公顷,规划10年后粮食单产比现在增加22%,人均粮食占有量比现在提高10%.如果人口年增长率为1%,那么耕地平均每年至多只能减少多少公顷(精确到1公顷)?

(24)(本小题满分12分)

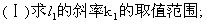
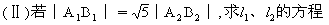
(25)(本小题满分12分)

已知a、b、c是实数,函数f(x)=ax²+bx+c,g(x)=ax+b,当-1≤x≤1时,│f(x)│≤1.

(Ⅰ)证明:│c│≤l;

(Ⅱ)证明:当-1≤x≤1时,│g(x)│≤2;

(Ⅲ)设a>0,当-1≤x≤1时,g(x)的最大值为2,求f(x).

(16)已知圆x²+y²-6x-7=0与抛物线y²=2px(p>0)的准线相切.则P=　　　　　　　　　　　　 .

(17)正六边形的中心和顶点共7个点,以其中3个点为顶点的三角形共有　　　 个(用数字作答).

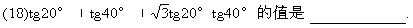
(19)如图,正方形ABCD所在平面与正方形ABEF所在平面成60°的二面角,则异面直线AD与BF所成角的余弦值是　　　　　　　 .

(1)已知全集I=N,集合A={x│x=2n,n∈N},B={x│x=4n,n∈N},则

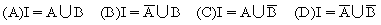
(2)当a>1时,在同一坐标系中,函数y=a^-x与y=log_ax的图象是

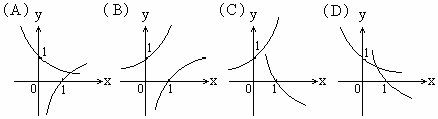
(3)若sin²x>cos²x,则x的取值范围是

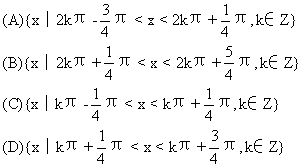
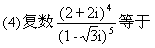
(A)α⊥γ且l⊥m　　　　　　　　　 　　　　(B)α⊥γ且m∥β

(C)m∥β且l⊥m　　　　　　　　　　　　　 (D)α∥β且α⊥γ

(A)(-3,5),(-3,-3)　　　　　　　　　　　　　 (B)(3,3,),(3,-5)

(C)(1,1,),(-7,1)　　　　　　　　　　　　　　 (D)(7,-1,),(-1,-1)

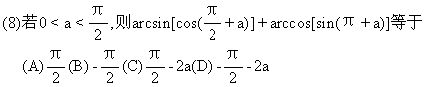
(9)将边长为a的正方形ABCD沿对角线AC折起,使得BD=a,则三棱锥D-ABC的体积为

(12)等差数列{a_n的前m项和为30,前2m项和为100,则它的前3m项和为

(A)130　　　　　　　 (B)170　　　　　　　　　　　 (C)210　　　　　　　　 (D)260

(14)母线长为1的圆锥体积最大时,其侧面展开图圆心角ψ等于

(15)设f(x)是(-∞,+∞)上的奇函数,f(x+2)=f(x),当0≤x≤1时,f(x)=x,则f(7.5)等于

(A)0.5　　　　　　　　　　　　　　　　　 (B)-0.5

(C)1.5　　　　　　　　　　　　　　　　　 (D)-1.5

第Ⅱ卷

(20)(本小题满分10分)

(21)(本小题满分11分)

(22)(本小题满分12分)

甲、乙两地相距S千米,汽车从甲地匀速行驶到乙地,速度不得超过c千米/时.已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v(千米/时)的平方成正比,且比例系数为b;固定部分为a元.

(Ⅰ)把全程运输成本y(元)表示为速度v(千米/时)的函数,并指出这个函数的定义域;

(Ⅱ)为了使全程运输成本最小,汽车应以多大速度行驶？

(23)(本小题满分12分)

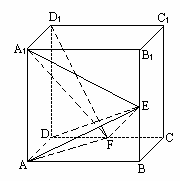
如图,在正方体ABCD-A₁B₁C₁D₁中,E、F分别是BB₁、CD的中点.

(Ⅰ)证明AD⊥D₁F;

(Ⅱ)求AE与D₁F所成的角;

(Ⅲ)证明面AED⊥面A₁FD₁;

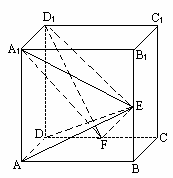
(Ⅳ)设AA₁=2,求三棱锥E-AA₁F的体积V_E-AA1F.

(24)(本小题满分12分)

已知过原点O的一条直线与函数y=log₈x的图象交于A、B两点,分别过点A、B作y轴的平行线与函数y=log₂x的图象交于C、D两点.

(Ⅰ)证明点C、D和原点O在同一条直线上;

(Ⅱ)当BC平行于x轴时,求点A的坐标.

(25)(本小题满分12分)

(17)已知直线x-y=2与抛物线y²=4x交于A、B两点,那么线段AB的中点坐标是__________.

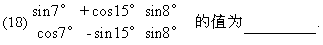
(19)已知m、l是直线，α、β是平面,给出下列命题:

①若l垂直于α内的两条相交直线,则l⊥α;

②若l平行于α,则l平行于α内的所有直线;

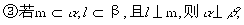
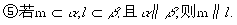
其中正确的命题的序号是______________.(注：把你认为正确的命题的序号都填上)

(1)设集合M={x│0≤x<2},集合N={x│x²-2x-3<0},集合M∩N=

(A){x│0≤x<1}　　　　　　　　　　　　　　　　 (B){x│0≤x<2}

(C){x│0≤x≤1}　　　　　　　　　　　　　 　　(D){x│0≤x≤2}

(2)如果直线ax+2y+2=0与直线3x-y-2=0平行,那么系数a=

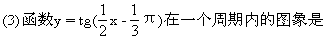
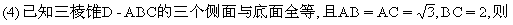
以BC为棱,以面BCD与面BCA为面的二面角的大小是

(6)满足tga≥ctga的角a的一个取值区间是

(7)设函数y=f(x)定义在实数集上,则函数y=f(x-1)与y=f(1-x)的图象关于

(A)直线y=0对称　　　　　　　　　　　　　　　 (B)直线x=0对称

(C)直线y=1对称　　　　　　　　　　　　　 　　(D)直线x=1对称

(8)长方体一个项点上三条棱的长分别是3,4,5,且它的八个顶点都在同一个球面上,这个球的表面积是

(9)如果直线l将圆:x²+y²-2x-4y=0平分,且不通过第四象限,那么l的斜率的取值范围是

(10)函数y=cos²x-3cosx+2的最小值为

是

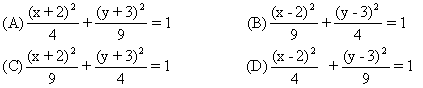
(12)圆台上、下底面积分别为π、4π,侧面积为6π,这个圆台的体积是

(13)定义在区间(-∞,+∞)的奇函数f(x)为增函数;偶函数g(x)在区间[0,+∞]的图象与f(x)的图象重合.设a>b>0,给出下列不等式

①f(b)-f(-a)>g(a)-g(-b);　　　　 ②f(b)-f(-a)<g(a)-g(-b);

③f(a)-f(-b)>g(b)-g(-a)　　④f(a)-f(-b)<g(b)-g(-a).

其中成立的是

(A)①与④　　　　 (B)②与③　　　 (C)①与③　　　 (D)②与④

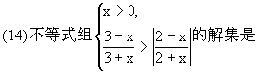
(15)四面体的一个顶点为A,从其它项点与各棱的中点中取3个点,使它们和点A在同一平面上,不同的取法有

(A)30种　　　　　 (B)33种　　　　 (C)36种　　　　 (D)39种

第Ⅱ卷

　(20)(本小题满分10分)

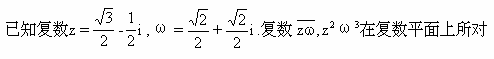
应的点分别为P,Q.证明△OPQ是等腰直角三角形(其中O为原点).

(21)(本小题满分11分)

已知数列{a_n},{b_n}都是由正数组成的等比数列,公比分别为p,q,其中p>q,且p≠1,q≠1.设c_n=a_n+b_n,s_n为数列{c_n}的前n项和.求

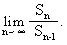
　(22)(本小题满分12分)

甲、乙两地相距S千米,汽车从甲地匀速行驶到乙地,速度不得超过c千米/时.已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v(千米/时)的平方成正比,比例系数为b;固定部分为a元.

(Ⅰ)全程运输成本把y(元)表示为速度v(千米/时)的函数,并指出这个函数的定义域;

(Ⅱ)为了使全程运输成本最小,汽车应以多大速度行驶?

　(23)(本小题满分12分)

如图,在正方体ABCD-A₁B₁C₁D₁中,E、F分别是BB₁、CD的中点.

(Ⅰ)证明AD⊥D₁F;

(Ⅱ)求AE与D₁F所成的角;

(Ⅲ)证明面AED⊥面A₁FD₁;

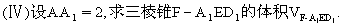
　(24)(本小题满分12分)

设二次函数f(x)=ax²+bx+c(a>0),方程f(x)-x=0的两个根x₁,x₂满足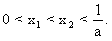

(Ⅰ)当x∈(0,x₁)时,证明x<f(x)<x₁;

.

(25)(本小题满分12分)

设圆满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长的比为3:1,在满足条件①、②的所有圆中,求圆心到直线ι:x-2y=0的距离最小的圆的方程.

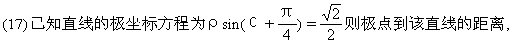
是___________.

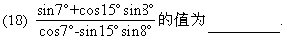
(19)已知m、l是直线,α、β是平面,给出下列命题:

①若l垂直于α内的两条相交直线,则l⊥α;

②若l平行于α,则l平行于α内的所有直线;

③若m α, l β,且l⊥m,则α⊥β;

④若l β,且l⊥α,则α⊥β;

⑤若m α, l β,且α∥β,则m∥l.

其中正确的命题的序号是___________.(注:把你认为正确的命题的序号都填上)

(1)设集合M={x│0≤x<2},集合N={x│x²-2x-3<0},集合M∩N=

(A){x│0≤x<1}　　　　　　　　　　　　　 (B){x│0≤x<2}

(C){x│0≤x≤1}　　　　　　　　　　　　 (D){x│0≤x≤2}

(2)如果直线ax+2y+2=0与直线3x-y-2=0平行,那么系数a=

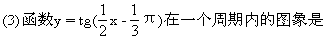
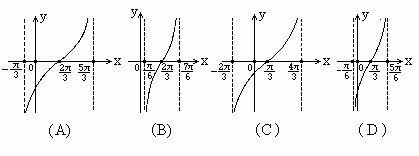
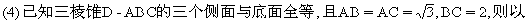
BC为棱,以面BCD与面BCA为面的二面角的大小是

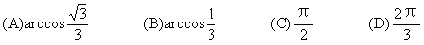
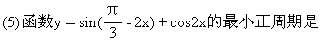
(6)满足arccos(1-x)≥arccosx的x的取值范围是

(7)将y=2^x的图象

(A)先向左平行移动1个单位　　　　　　　　 (B)先向右平行移动1个单位

(C)先向上平行移动1个单位　　　　　　　 (D)先向下平行移动1个单位

再作关于直线y=x对称的图象,可得到函数y=log₂(x+1)的图象.

(8)长方体一个顶点上三条棱的长分别是3,4,5,且它的八个顶点都在同一个球面上,这个球的表面积是

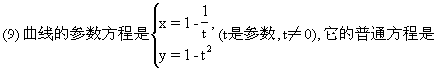
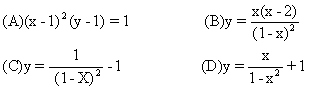
(10)函数y=cos²x-3cosx+2的最小值为

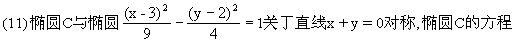
(12)圆台上、下底面积分别为π、4π,侧面积为6π,这个圆台的体积是

(13)定义在区间(-∞,+∞)的奇函数f(x)为增函数；偶函数g(x)在区间［0,+∞)的图象与f(x)的图象重合.设a>b>0,给出下列不等式:

①f(b)-f(-a)>g(a)-g(-b);　　　　　　　　 ②f(b)-f(-a)<g(a)-g(-b);

③f(a)-f(-b)>g(b)-g(-a);　　　　　　　　　 ④f(a)-f(-b)<g(b)-g(-a),

其中成立的是

(A)①与④　　　　　 (B)②与③　　　　　 (C)①与③　　　 (D)②与④

(15)四面体的顶点和各棱中点共10个点,在其中取4个不共面的点,不同的取法共有

(A)150种　　　　　　 (B)147种　　　　　　　　 (C)144种　　　　　　 (D)141种

第Ⅱ卷