21、飞船返回仓顺利到达地球后，为了及时将航天员救出，地面指挥中心在返回仓预计到达区域安排三个救援中心(记为A，B，C)，B在A的正东方向，相距6km,C在B的北偏东30⁰，相距4km,P为航天员着陆点，某一时刻A接到P的求救信号，由于B、C两地比A距P远，因此4s后，B、C两个救援中心才同时接收到这一信号，已知该信号的传播速度为1km/s.

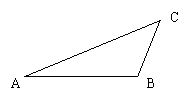(1)求A、C两个救援中心的距离；

(2)求在A处发现P的方向角；

(3)若信号从P点的正上方Q点处发出，则A、B

收到信号的时间差变大还是变小，并证明你的结论.

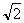20、如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB=，AF=1，M是线段EF的中点.

(1)求证AM//平面BDE； (2)求二面角A-DF-B的大小；

(3)试在线段AC上确定一点P，使得PF与BC所成的角是 60°.

19、甲乙两人独立解某一道数学题，已知该题被甲独立解出的概率为0.6，被甲或乙解出的概率为0.92.

(1)求该题被乙独立解出的概率；

(2)求解出该题的人数的数学期望和方差.

18、现有A、B、C、D四个长方体容器，A、B的底面积均为x，高分别为x,y; C、D的底面积均为y，高也分别为x、y(其中x≠y).现规定一种两人的游戏规则：每人从四种容器中取两个盛水，盛水多者为胜，问先取者在未能确定x与y大小的情况下有没有必胜的方案？若有的话，有几种？

17、设函数f(x)=m·n，其中向量m=(2cosx,1),n=(cosx,sin2x),x∈R.

(1)　　　 求f(x)的最小正周期；

(2)　　　 在△ABC中，a、b、c分别是角A、B、C的对边，f(A)=2,a=,b+c=3(b＞c),求b、c的长.

16、已知f(x)是定义在R上的不恒为零的函数，且对于任意的a、b∈R，满足f(a·b)=af(b)+bf(a),f(2)=2,a=(n∈N,b∈N.考查下列结论:①f(0)=f(1);②f(x)为偶函数；③数列{a为等比数列；④{b为等差数列.

其中正确的是____________.

15、=___________.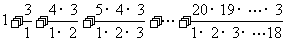

14、设x,y满足则该不等式组表示的平面区域的面积为________ ;z=2x+y的最大值是________________.

13、在的展开式中，常数项是　　　　　　　　

12、在1，2，3，4，5的排列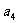，，，，，中，满足 <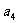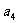，>，<，>的排列个数是 　　　　　　　　　

A．10　　　　　　　 B．12　　　　　　　　　 C．14　　　　　　　　 D．16