
5.已知函数 (
(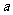 >0,
>0, ),且
),且 ,则
(
)
,则
(
)
(A) >
> (B)
(B)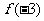 >
> (C)
(C) >
> (D)
(D)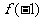 >
>
4.已知 ,则“
,则“ ”是“
”是“ ”的
( )
”的
( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
3.函数 (
(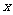 >0)的反函数是
( )
>0)的反函数是
( )
(A) (
( )
(B)
)
(B)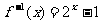 (
( )
)
(C) (
( >0)
(D)
>0)
(D)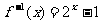 (
( >0)
>0)
2.在等差数列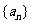 中,若
中,若 ,则
,则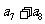 的和等于
( )
的和等于
( )
(A)7 (B)8 (C)9 (D)10
1.已知全集I=R,集合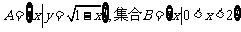 ,则
,则 等于( )
等于( )
(A) (B)
(B) (C)
(C) (D)
(D)
(17)(本题12分)解不等式 .
.
(18)(本题12分)已知向量 ,
, 。
。
(I)若 ,求
,求 ;
;
(II)求 的最大值。
的最大值。
(19)、(本题12分)在 中,
中, ,
, ,
,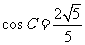 。
。
(1) 求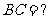
(2) 若点D是AB中点,求中线CD的长度。
(20)(本题12分)已知圆内接四边形ABCD的边长分别为AB=2,BC=6,CD=DA=4,求四边形ABCD的面积.
(21)(本题12分)若 是公差不为0的等差数列
是公差不为0的等差数列 的前
的前 项和,且
项和,且 ,
, ,
, 成等比数列.
成等比数列.
(Ⅰ)求数列 ,
, ,
, 的公比;
的公比;
(Ⅱ)若 ,求
,求 的通项公式.
的通项公式.
(22)(本题14分)设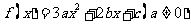 ,若
,若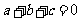 ,
, ,求证:
,求证:
(Ⅰ)方程 有实根;
有实根;
(Ⅱ) ;
;
(Ⅲ)设 ,
,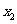 是方程
是方程 的两个实根,则
的两个实根,则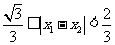 .
.
(13)函数 的最小正周期是___________________;
的最小正周期是___________________;
(14)设向量 ,
, ,且
,且 ,那么
,那么 与
与 夹角的大小是_______________________;
夹角的大小是_______________________;
(15)不等式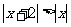 的解集为_____________________________________;
的解集为_____________________________________;
(16)若互不相等的实数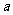 、
、 、
、 成等差数列,
成等差数列, 、
、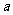 、
、 成等比数列,且
成等比数列,且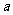 +
+ +
+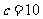 ,则
,则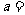 ______________________。
______________________。
(1)设集合M={x|x2-x<0},N={x||x|<2},则
(A)M∩N= (B)M∩N=M (C)M∪N=M (D)M∪N=R
(B)M∩N=M (C)M∪N=M (D)M∪N=R
(2)函数 的定义域是
的定义域是
(A) (0,1] (B)(0,+∞) (C)(1,+∞) (D)[1,+∞)
(3) 若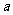 、b、c∈R,
、b、c∈R, ,则下列不等式成立的是
,则下列不等式成立的是
(A) (B)
(B) 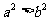
(C)  (D)
(D)
(4)为了得到函数 的图像,只需把函数
的图像,只需把函数 的图像上所有的点
的图像上所有的点
(A)向左平移 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 倍(纵坐标不变)
倍(纵坐标不变)
(B)向右平移 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 倍(纵坐标不变)
倍(纵坐标不变)
(C)向左平移 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
(D)向右平移 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
(5)已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为
(A)6 (B)5 (C)4 (D)3
(6)若 与
与 都是非零向量,则“
都是非零向量,则“ ”是“
”是“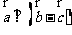 ”的
”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(7)设向量 ,
,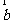 ,
, 满足
满足 ,且
,且 ⊥
⊥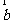 ,|
,| |=1,|
|=1,|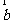 |=2,则
|=2,则
(A)1 (B)2 (C)4 (D)5
(8)已知 ,则
,则
(A)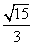 (B)
(B) (C)
(C) (D)
(D)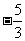
(9)设点P是函数 的图象C的一个对称中心,若点P到图象C的对称轴的距离的最小值是
的图象C的一个对称中心,若点P到图象C的对称轴的距离的最小值是 ,则
,则 的最小正周期是
的最小正周期是
(A)2π
(B)π (C)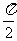 (D)
(D)
(10)已知向量 、
、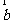 满足|
满足| |=1,|
|=1,|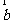 |=4,且
|=4,且 ·
·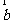 =2,则
=2,则 与
与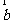 的夹角为
的夹角为
(A) (B)
(B) (C)
(C) (D)
(D)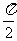
(11)不等式 的解集是
的解集是
(A) (B)
(B)  (C)
(C)  (D)
(D)
(12)若不等式 对一切
对一切 恒成立,则
恒成立,则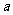 的最小值为
的最小值为
(A) (B)
(B) (C)
(C) (D)
(D)
选择题答题栏
第II卷(非选择题 共90分)
22. (14分) 22.已知数列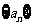 的首项
的首项 前
前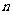 项和为
项和为 ,且
,且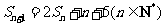
(I)证明数列 是等比数列;
是等比数列;
(II)令 ,求函数
,求函数 在点
在点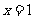 处的导数
处的导数 ,
,
并比较 与
与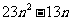 的大小.
的大小.
21. (12分)已知f(x)=ax3+bx2+cx+d(a≠0)是定义在R上的函数,其图象交x轴于A、B、C三点,若点B的坐标为(2,0)且f(x)在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
(Ⅰ)求实数c的值;
(Ⅱ)在函数f(x)图象上是否存在一点M(x0,y0),使f(x)在点M的切线斜率为3b?若存在,求出点M的坐标;不存在说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com