
5.要从165人中抽取15人进行身体健康检查,现采用分层抽样法进行抽取,若这165人中,
老年人为22人,则老年人中被抽取参加健康检查的人数为 ( )
A.5 B.4 C.3 D.2
4.已知集合M={1,a2},P={-a,-1},若M∪P的元素个数为3,则M∩P= ( )
A.{0,1} B.{0,-1} C.{0} D.{-1}
3.sin20°cos70°+sin10°sin50°= ( )
A.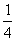 B.
B.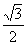 C.
C. D.
D.
2.已知f(x)=x2-4x+5在区间[0,5]上的最小值、最大值分别为a、b,则(a,b)是 ( )
A.(1,5) B.(1,10) C.(5,10) D.(2,1)
1.a表示“处理框”,b表示“输入、输出框”,c表示“起、止框”,d表示“判断框”,以下四个图形依次为 ( )

A.abcd B.dcab C.bacd D.cbad
22.(本小题满分14分)
在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合(如图所示)。将矩形折叠,使A点落在线段DC上。
(1)若折痕所在直线的斜率为k,试写出折痕所在直线的方程;
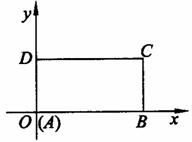 (2)设折痕所在直线与y轴交于点F,过点E、D、F的圆被y轴分得的两段弧长的比为1 :5,求圆的方程。
(2)设折痕所在直线与y轴交于点F,过点E、D、F的圆被y轴分得的两段弧长的比为1 :5,求圆的方程。
21.(本小题满分12分)
设函数 其中
其中
(1)求函数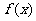 的最值;
的最值;
(2)判断,当 时,函数
时,函数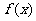 在区间
在区间 内是否存在零点。
内是否存在零点。
20.(本小题满分12分)
如图是某多面体的三视图,如果图中每个正方形的边长为2。
 (1)请描述满足该三视图的一个几
(1)请描述满足该三视图的一个几
何的形状(或画出它的直观图);
(2)求你得到的几何体的体积;
(3)求你得到几何体的表面积。
19.(本小题满分12分)
某种洗衣机洗涤衣服时,需经过进水、清洗、排水、脱水四个连续的过程。假设进水时水量匀速增加,清洗时水量保持不变。已知进水时间为4分钟,清洗时间为12分钟,排水时间为2分钟,脱水时间为2分钟。洗衣机中的水量y(升)与时间x(分钟)之间的关系如下表所示:
|
x |
0 |
2 |
4 |
16 |
16.5 |
17 |
18 |
… |
|
y |
0 |
20 |
40 |
40 |
29.5 |
20 |
2 |
… |
请根据表中提供的信息解答下列问题:
 (1)试写出当
(1)试写出当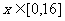 时y关于x的函数解析式,并画出该函数的图象;
时y关于x的函数解析式,并画出该函数的图象;
(2)根据排水阶段的2分钟点(x,y)的分布情况,
可选用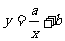 或
或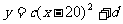 (其中
(其中
a、b、c、d为常数),作为在排水阶段的2分钟
内水量y与时间x之间关系的模拟函数。试分别
求出这两个函数的解析式;
18.(本小题满分12分)
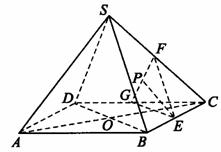 在正四棱锥S-ABCD中,E、F、G分别是BC、SC和DC的中点,P眯在线段FG上。
在正四棱锥S-ABCD中,E、F、G分别是BC、SC和DC的中点,P眯在线段FG上。
求证:(1)平面EFG//平面SDB;
(2)PE⊥AC。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com