
4、已知数列 满足
满足 =1,
=1,
 且
且  , 则
, 则  等于
等于
(A) (B) (C) (D)
3.设直线ax+by+c=0的倾斜角为 ,且sin
,且sin cos
cos =0,则a,b满足(
)
=0,则a,b满足(
)
A.a+b=1 B.a b=1 C.a+b=0 D.a
b=1 C.a+b=0 D.a b=0
b=0
2、D是△ABC的边AB上靠近A点的三等分点,则向量 等于( )
等于( )
A 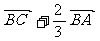 B
B 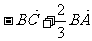 C
C  D
D 
1.sin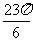 的值是( )
的值是( )
A. B.
B. C.
C. D.
D.
22.(本小题满分14分)
已知函数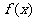 是定义在[-2,2]上奇函数,当x∈
是定义在[-2,2]上奇函数,当x∈ (t为常数).
(t为常数).
(1)求函数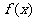 的解析式;
的解析式;
(2)当t∈[2,6]时,求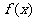 在[-2,0]上的最小值以及取得最小值时的x值;
在[-2,0]上的最小值以及取得最小值时的x值;
(3)当t≥9时,证明函数y=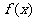 的图象上至少有一个点落在直线y=14上.
的图象上至少有一个点落在直线y=14上.
21.(本小题满分12分)
已知圆C的方程为 .
.
(1)若圆C的切线在x轴的正半轴和y轴的正半轴上的截距相等,求此切线的方程;
(2)从圆C外一点P(x,y)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求P点的轨迹方程.
(3)在(2)的条件下,求使得|PM|取得最小值的点P的坐标.
20.(本小题满分12分)
 已知:如图,AB是圆柱下底面圆O2的直径,PA是圆柱的一条母线,C是圆柱下底面圆O2圆周上一点.
已知:如图,AB是圆柱下底面圆O2的直径,PA是圆柱的一条母线,C是圆柱下底面圆O2圆周上一点.
|
(2)若C恰为AB的中点,按图
中所给尺寸,计算三棱锥
B-PAC的体积.
19.(本小题满分12分)
已知函数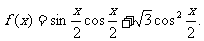
(1)求当x∈[0,π]时,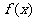 的零点;
的零点;
(2)求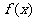 的值域;
的值域;
(3)将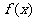 的图象经过怎样的平移,使得平移后的图象关于原点对称?(只需说出一
的图象经过怎样的平移,使得平移后的图象关于原点对称?(只需说出一
种平移途径即可)
18.(本小题满分12分)
 济南市某公交线路某区间的内共设置六个站点(如图所示),分别记为A0、A1、A2、A3、A4、A5,现有甲、乙两人同时从A0站点上车,且他们中的每个人在站点Ai=(i=1,2,3,4,5)下车是等可能的.
济南市某公交线路某区间的内共设置六个站点(如图所示),分别记为A0、A1、A2、A3、A4、A5,现有甲、乙两人同时从A0站点上车,且他们中的每个人在站点Ai=(i=1,2,3,4,5)下车是等可能的.
求:(1)甲在A2站点下车的概率;
(2)甲、乙两人不在同一站点下车的概率.
17.(本小题满分12分)
设函数 ,如果
,如果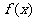 >1,求x的取值范围
>1,求x的取值范围
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com