
2.sin17°sin223°+sin73°sin47°等于 ( )
A.- B.
B. C.-
C.- D.
D.
1.若U={1,2,3,4},M={1,2}, N={2,3}则CU(M∪N)= ( )
A.{1,2,3} B.{2} C.{1,2,3} D.{4}
17 (本题满分12分)
(文)如图,已知圆A的半径是2,圆外一定点N与圆A上的点的最短距离为6,
 过动点P作A的切线PM(M为切点),连结PN使得PM:PN=
过动点P作A的切线PM(M为切点),连结PN使得PM:PN= ,试建立适当的坐标系,求动点P的轨迹
,试建立适当的坐标系,求动点P的轨迹
(理)设有关于x的不等式 a
a
(I)当a=1时,解此不等式
(II)当a为何值时,此不等式的解集是R
18 (本题满分12分)
(文)已知 ,求
,求 和
和 的值
的值
(理)已知二次函数 的二次项系数为
的二次项系数为 ,且不等式
,且不等式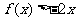 的解集为
的解集为
(I)若方程 有两个相等的实数根,求
有两个相等的实数根,求 的解析式;
的解析式;
(II)若函数 的无极值,求实数
的无极值,求实数 的取值范围
的取值范围
19 (本题满分12分)
(文)设有关于x的不等式 a
a
(I)当a=1时,解此不等式
(II)当a为何值时,此不等式的解集是R
(理)如图,已知圆A的半径是2,圆外一定点N与圆A上的点的最短距离为6,
 过动点P作A的切线PM(M为切点),连结PN使得PM:PN=
过动点P作A的切线PM(M为切点),连结PN使得PM:PN= ,试建立适当的坐标系,求动点P的轨迹
,试建立适当的坐标系,求动点P的轨迹
20 (本题满分12分)
(文)已知二次函数 的二次项系数为
的二次项系数为 ,且不等式
,且不等式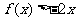 的解集为
的解集为
(I)若方程 有两个相等的实数根,求
有两个相等的实数根,求 的解析式;
的解析式;
(II)若函数 的无极值,求实数
的无极值,求实数 的取值范围
的取值范围
(理)已知向量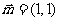 ,向量
,向量 与向量
与向量 的夹角为
的夹角为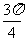 ,且
,且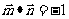
(I)求向量
(II)若向量 与向量
与向量 的夹角为
的夹角为 ,向量
,向量 ,其中A,C为△ABC的内角,且B=600,求
,其中A,C为△ABC的内角,且B=600,求 的取值范围
的取值范围
21 (本题满分14分)
已知数列{an}的前n项和为Sn,且an= (3n+Sn)对一切正整数n成立
(3n+Sn)对一切正整数n成立
(I)证明:数列{3+an}是等比数列,并求出数列{an}的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前n项和Bn;
的前n项和Bn;
(Ⅲ)数列{an}中是否存在构成等差数列的四项?若存在求出一组;否则说明理由
22 (本题满分14分)
如图,已知椭圆 过其左焦点且斜率为1的直线与椭圆及其准线的交点从左到右的顺序为A、B、C、D,设
过其左焦点且斜率为1的直线与椭圆及其准线的交点从左到右的顺序为A、B、C、D,设
①求 的解析式;
的解析式;
②求 的最值
的最值
11 (文)命题“若 ,则
,则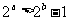 ”的否命题为
”的否命题为
(理)如果椭圆的对称轴为坐标轴,短轴的一个端点与两焦点组成一正三角形,焦点在y轴上,且a-c=, 那么椭圆的方程是
12 (文) 的值是
的值是
(理)函数 的反函数
的反函数 是
是
13 (文)如果椭圆的对称轴为坐标轴,短轴的一个端点与两焦点组成一正三角形,焦点在y轴上,且a-c=, 那么椭圆的方程是
(理)已知直线ax+by+c=0被圆M: 所截得的弦AB的长为
所截得的弦AB的长为 ,那么
,那么
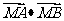 的值等于
的值等于
14 已知直线ax+by+c=0被圆M: 所截得的弦AB的长为
所截得的弦AB的长为 ,那么
,那么
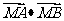 的值等于
的值等于
15 已知函数 设
设 ,则使
,则使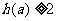 成立的
成立的 的范围是
的范围是
16 有 以下几个命题
①曲线 按
按 平移可得曲线
平移可得曲线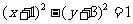 ;
;
②若|x|+|y| ,则使x+y取得最大值和最小值的最优解都有无数多个;
,则使x+y取得最大值和最小值的最优解都有无数多个;
③设A、B为两个定点,为常数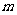 ,
, ,则动点P的轨迹为椭圆;
,则动点P的轨迹为椭圆;
④若椭圆的左、右焦点分别为F1、F2,P是该椭圆上的任意一点,则点F2关于“ 的外角平分线”的对称点M的轨迹是圆
的外角平分线”的对称点M的轨迹是圆
其中真命题的序号为 ;(写出所有真命题的序号)
1 设集合P={直线的倾斜角},Q={两个向量的夹角},R={两条直线的夹角},M={直线l1到l2的角}则必有
A Q R=P
R=P M B R
M B R M
M P
P Q C Q=R
Q C Q=R M=P D R
M=P D R P
P M
M Q
Q
2 在等差数列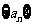 中,若
中,若 ,则其前n项和
,则其前n项和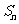 的值等于5C的是
的值等于5C的是
A 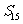 B
B 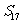 C
C  D
D 
3 (文)若点B分 的比为
的比为 ,且有
,且有 ,则
,则 等于
等于
A 2
B  C 1
D -1
C 1
D -1
(理)函数 是
是
A 周期为 的奇函数
B
周期为
的奇函数
B
周期为 的偶函数
的偶函数
C 周期为 的奇函数
D 周期为
的奇函数
D 周期为 的偶函数
的偶函数
4 过点(-4,0)作直线L与圆x2+y2+2x-4y-20=0交于A、B两点,如果|AB|=8,
则L的方程为
A 5x+12y+20=0 B 5x-12y+20=0
C 5x-12y+20=0或x+4=0 D 5x+12y+20=0或x+4=0
5 (文)已知p, q,
p+q是等差数列,p ,q ,pq是等比数列,则椭圆 的准线方程是
的准线方程是
A  B
B 
C  D
D 
(理)已知命题P:关于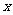 的不等式
的不等式 的解集为
的解集为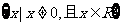 ;命题Q:
;命题Q: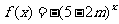 是减函数 若P或Q为真命题,P且Q为假命题,则实数
是减函数 若P或Q为真命题,P且Q为假命题,则实数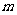 的取值范围是
的取值范围是
A (1,2) B  1,2)
C (-
1,2)
C (- ,1
,1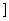 D (-
D (- ,1)
,1)
6 (文)已知命题P:关于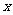 的不等式
的不等式 的解集为
的解集为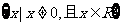 ;命题Q:
;命题Q: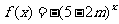 是减函数 若P或Q为真命题,P且Q为假命题,则实数
是减函数 若P或Q为真命题,P且Q为假命题,则实数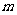 的取值范围是
的取值范围是
A (1,2) B  1,2)
C (-
1,2)
C (- ,1
,1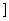 D (-
D (- ,1)
,1)
(理)若点B分 的比为
的比为 ,且有
,且有 ,则
,则 等于
等于
A 2 B  C 1
D -1
C 1
D -1
7 (文)函数 是
是
A 周期为 的奇函数
B 周期为
的奇函数
B 周期为 的偶函数
的偶函数
C 周期为 的奇函数
D 周期为
的奇函数
D 周期为 的偶函数
的偶函数
(理)若 ,对任意实数
,对任意实数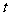 都有
都有 ,且
,且 , 则实数
, 则实数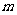 的值等于
的值等于
A  B
B  C -3或1 D -1或3
C -3或1 D -1或3
8 (文)若 ,对任意实数
,对任意实数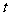 都有
都有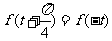 ,且
,且 , 则实数
, 则实数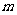 的值等于
的值等于
A  B
B  C -3或1 D -1或3
C -3或1 D -1或3
(理)设函数 ,数列
,数列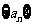 是公比为
是公比为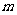 的等比数列,若
的等比数列,若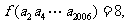 则
则 的值等于
的值等于
A -1974 B -1990 C 2022 D 2038
9 (文)设函数 ,数列
,数列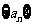 是公比为
是公比为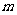 的等比数列,若
的等比数列,若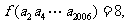 则
则 的值等于
的值等于
A -1974 B -1990 C 2022 D 2038
(理)函数 是奇函数,且在R上是增函数的充要条件是
是奇函数,且在R上是增函数的充要条件是
A p>0 ,q=0 B p<0 ,q=0 C p≤0,q=0 D p≥0,q=0
10 (文)函数 是奇函数,且在R上是增函数的充要条件是
是奇函数,且在R上是增函数的充要条件是
A p>0 ,q=0 B p<0 ,q=0 C p≤0,q=0 D p≥0,q=0
(理)已知函数 满足:①
满足:①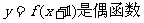 ;②在
;②在 上为增函数
上为增函数
若 ,且
,且 ,则
,则 与
与 的大小关系是
的大小关系是
A  B
B 
C  D 无法确定
D 无法确定
第Ⅱ卷 (非选择题,共100分)
(17)(本小题满分12分)
在△ABC中,角A、B、C所对的边分别是a、b、c,则 ·
·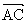 =
=  S△ABC(其中S△ABC 为△ABC的面积).
S△ABC(其中S△ABC 为△ABC的面积).
(I)求sin2 +cos2A;
+cos2A;
(Ⅱ)若b=2, △ABC的面积S△ABC =3,求a.
(18) (本小题满分12分)
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面ABF是等边三角形,

|
 BC.
BC.
(I)证明肋∥平面ABF;
(Ⅱ)问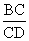 为何值时,有DF⊥平面ABE,
为何值时,有DF⊥平面ABE,
试证明你的结论.
(19)(本小题满分12分)
甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头,它们在一昼夜内任何时刻到达是
等可能的.
(I)如果甲船和乙船的停泊时间都是4小时,求它们中的任何一条船不需要等待码头空出的概率;
(Ⅱ)如果甲船的停泊时间为4小时,乙船的停泊时间是2小时,求它们中的任何一条船不
需要等待码头空出的概率.
(20) (本小题满分12分)
函数y= f(x)是定义域为R的奇函数,且对任意的 ,均有f(x+4)
= f(x)成立.当
,均有f(x+4)
= f(x)成立.当 时,f(x)=
一x2+2x+1.
时,f(x)=
一x2+2x+1.
(I)当x ∈[4 k一2, 4k+2] (k∈Z)时,求函数f(x) 的表达式;
(Ⅱ)求不等式f(x)
> 的解集.
的解集.
(21) (本小题满分12分)
设数列{an}的各项都是正数,且对任意n ∈ N*,都有a13+a23+a33+…+an 3=Sn2,其中Sn为数列{an}的前n项和.
(I) 求证:an2 =2 Sn -an;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)设bn=3n+(一1) n-1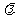 ·
·  (
(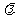 为非零整数,n∈N*),试确定
为非零整数,n∈N*),试确定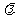 的值,使得对任意n∈
的值,使得对任意n∈
N*,都有bn+1。>bn成立.
(22) (本小题满分14分)
如图,已知椭圆C: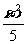 +
+ =
= m>0),经过椭圆C的右焦点,且斜率为k(k≠0)的直
m>0),经过椭圆C的右焦点,且斜率为k(k≠0)的直
线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.
(Ⅰ)是否存在k,使对任意m>o,总有 +
+ =
=  成立?若存在,求出所有k的值;
成立?若存在,求出所有k的值;
(Ⅱ)若 ·
· = 一
= 一  (m3+4 m),求实数k的取值范围.
(m3+4 m),求实数k的取值范围.

(13)已知一圆锥的侧面展开图为半圆,且面积为S,则圆锥的底面面积是 .
(14)一个总体中有100个个体,随机编号0,l,2,…,99,依从小到大的编号顺序平均分成10个小组,组号依次为1,2,3,…,10.现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k组中抽取的号码个位数字与m+k的个位数字相同,若m=8,则在第8组中抽取的号码是 .
(15)某商场在节假日对顾客购物实行一定的优惠,商场规定:
①如一次购物不超过200元,不给予折扣;
②如一次购物超过200元不超过500元,按标准价给予九折优惠;
③如一次购物超过500元的,其中500元给予九折优惠,超过500元的剩余部分给予八五
折优惠.
某人两次去购物,分别付款176元和432元.如果他只去一次购买同样的商品,则他应该
付款为 元.
(16)设函数f(x)=sin( x+
x+  ) (
) ( >0,-
>0,-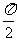 <
< <
<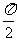 ),有下列论断:
),有下列论断:
① f(x) 的图象关于直线x =  对称;
对称;
② f(x) 的图象关于( ,0)对称;
,0)对称;
③ f(x) 的最小正周期为 ;
;
④在区间[一 ,0]上,f(x)为增函数.
,0]上,f(x)为增函数.
以其中的两个论断为条件,剩下的两个论断为结论,写出你认为正确的一个命题:若
,则 .(填序号即可)
符合题目要求的.
(1)已知集合M={0,a},N=| x |
x2-2x一3<0,x∈Z | , 若M∩N≠ ,则a的值为
,则a的值为
(A)1 (B)2 (C)1或2 (D)不为零的任意实数
(2)下列函数中既是奇函数,又在区间(0,+∞)上单调递增的是
(A)y=sinx (B)y= 一x2 (C)y=lg2x (D)y=e| x |
(3)若cos(2 )=
)= 且a∈(一
且a∈(一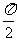 , 0),则sin(
, 0),则sin( 一
一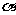 )
)
(A)一 (B)一
(B)一 (C)一
(C)一 (D)±
(D)±
(4)给出以下命题:① , x4>x2;②
, x4>x2;②  ,使得sin3
,使得sin3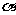 =3sin
=3sin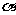 ;③
;③ ,对
,对
使x2+2x+a<0.其中真命题的个数为
(A) 0 (B) 1 (C) 2 ( D) 3
(5)若x∈(0,1),则下列结论正确的是
(A)2x> > lgx (B) 2x >
lgx >
> lgx (B) 2x >
lgx >
(C) >2x>lgx (D)lgx>
>2x>lgx (D)lgx> >2x
>2x
(6)一块各面均涂有油漆的正方体被锯成1000个大小相同的小正方体,若将这些小正方体均匀地搅混在一起,则任意取出一个正方体其两面涂有油漆的概率是
(A) 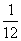 (B)
(B) 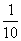 (C)
(C) 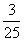 (D)
(D) 
(7)把直线x一2y+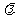 =0向左平移1个单位,再向下平移2个单位后,与曲线x2+y2+2x一4y =0正好相切,则实数
=0向左平移1个单位,再向下平移2个单位后,与曲线x2+y2+2x一4y =0正好相切,则实数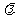 的值为
的值为
(A) -13或3 (B)13或-3 (C)13或3 (D) -13或 -3
 (8)已知函数y=f(x)在(0,1)内的一段图象是如图所示的一段
(8)已知函数y=f(x)在(0,1)内的一段图象是如图所示的一段
圆弧,若0<x1<x2<1,则
(A)  <
<  (B)
(B)  =
= 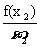
(C)  >
>  (D)不能确定
(D)不能确定
 (9)如图,三棱锥P-ABC中,PA=PB=PC 且△ABC为正三角
(9)如图,三棱锥P-ABC中,PA=PB=PC 且△ABC为正三角
形,M、N分别是PB、PC的中点,若截面AMN上侧面PBC,
则此棱锥侧面PBC与底面ABC所成二面角的余弦值是
(A)  (B)
(B)  (c)
(c)  (D)
(D) 
(10)在等比数列{an}中,a1=3 前n项和为Sn,若数列{an+1}也
是等比数列,则Sn等于
(A)2 n (B)3 n
(C)2n+1 (D)3n一1
(11)在△OAB中,  = a,
= a, =b,OD是AB边上的高,
=b,OD是AB边上的高, =
= 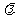
 ,则实数
,则实数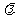 等于
等于
 (A)
(A)
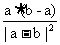 (B)
(B)  (C)
(C)  (D)
(D) 
(12)如图,过抛物线y2=2px (p>0) 的焦点F的直线l交抛物线于
点A、B,交其准线于点C,若| BC |=2 | BF |,且| AF|=39则此
抛物线的方程为
(A)y2=9 x (B)y2=6 x
(C)y2=3
x
(D)y2=  x
x
第Ⅱ卷(非选择题共90分)
(17)(本小题满分12分)
比较log(3x +1)与log(x一3)的大小.
(18)(本小题满分12分)
已知A、B、C是△ABC的三个内角,a,b,c为其对应边.向量 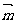 =(一1,
=(一1, ),
),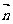 =(cosA,
=(cosA,
sinA),且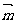 ·
·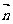 = 1.
= 1.
(I)求角A;
(Ⅱ)若  =(2,1),
=(2,1), 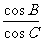 =
=  ,求△ABC的面积S.
,求△ABC的面积S.
(19)(本小题满分12分)
 如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面ABF是等边三角形,棱
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面ABF是等边三角形,棱
(20)(本小题满分12分)
某工厂统计资料显示,产品次品率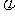 与日产量x(件) (x∈N且l≤x≤89)的关系符合如下规律:
与日产量x(件) (x∈N且l≤x≤89)的关系符合如下规律:
|
x |
1 |
2 |
3 |
4 |
… |
89 |
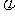 |
 |
 |
 |
 |
… |
 |
又知每生产一件正品盈利a元,每生产一件次品损失 元(a>o).
元(a>o).
(I)将该厂日盈利额T(元)表示为日产量x(件)的函数;
(Ⅱ)为了获得最大盈利,该厂的日产量应定为多少件?(取 ≈1.7计算).
≈1.7计算).
(21)(本小题满分12分)
已知圆O:x2+y2=1,把圆O上各点的纵坐标不变,横坐标伸长到原来的压倍,得到曲线
E.
(I)求曲线E的方程并指出曲线E是什么曲线;.
(Ⅱ)设F(一l,0),过点F且不与坐标轴垂直的直线交曲线E于A、B两点,线段AB的垂直平分线与x轴交于C点,求G点横坐标的取值范围.
(22)(本小题满分14分)
已知数列{an}满足:al=1,a2=2 , 2 an+2= [3+(一1)n]an一2[(一1)n一1],n∈N*.
(工)求a3,a4,a5,a6的值及数列{an}的通项公式;
(Ⅱ)设bn=a2n一l ·a2n,求数列{bn}的前n项和Sn.
(13)一个田径队,有男运动员56人,女运动员42人,比赛后,立即用分层抽样的方法,从全体队员中抽出一个容量为28的样本进行尿样兴奋剂检查,其中男运动员应抽 人.
(14)方程  +
+ =1的曲线是双曲线的充要条件是
.
=1的曲线是双曲线的充要条件是
.
 2x+y一2≥0
2x+y一2≥0
(15)已知 x一2y+4≥0, 则s=x2+y2的最大值是 .
3x一y一3≤0.
(16)一水池有2个进水口,1个出水口,每个进水口的进水速度如图甲,出水口的出水速度
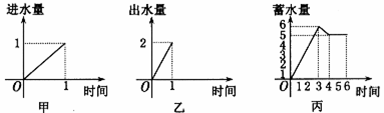 如图乙.某天0点到6点,该水池的蓄水量如图丙所示(至少打开一个水口).给出以下3个论断:
如图乙.某天0点到6点,该水池的蓄水量如图丙所示(至少打开一个水口).给出以下3个论断:
①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水.则一定能确定正确的论断是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com