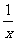1.若集合A={y│y=x,-1≤x≤1},B={y│y=2-,0<x≤1},则A∩B等于　　　

　 A. (-∞, -1]　　　　 　　　　　B. {1}　　 　　　　　　C.Φ　　　　　　 　　D. [-1,1]

22.已知点列B₁(1,y₁)、B₂(2,y₂)、…、B_n(n,y_n)(n∈N)

　　 顺次为一次函数图象上的点，

　 点列A₁(x₁,0)、A₂(x₂,0)、…、A_n(x_n,0)(n∈N)

　　 顺次为x轴正半轴上的点，其中x₁=a(0＜a＜1)，

　　 对于任意n∈N，点A_n、B_n、A_n+1构成以

　　 B_n为顶点的等腰三角形。

⑴求{y_n}的通项公式，且证明{y_n}是等差数列；

⑵试判断x_n+2-x_n是否为同一常数(不必证明)，并求出数列{x_n}的通项公式；

　　 ⑶在上述等腰三角形A_nB_nA_n+1中，是否存在直角三角形？若有，求出此时a值；若不存在，

　　　 请说明理由。

21.已知函数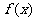是在上每一点均可导的函数，若在时恒成立.

(1)求证：函数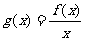在上是增函数；

(2)求证：当时，有；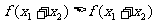

(3)请将(2)问推广到一般情况，并用数学归纳法证明你的结论.

20.设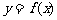是定义在上的函数，如果存在点，对函数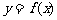的图像上任意点，关于点的对称点也在函数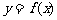的图像上，则称函数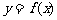关于点对称，称为函数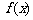的一个对称点. 对于定义在上的函数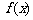，可以证明点是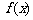图像的一个对称点的充要条件是,.

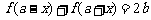(1) 求函数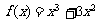图像的一个对称点；

(2)函数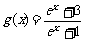的图像是否有对称点？若存在则求之，否则说明理由.

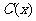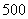19.某厂生产某种产品的年固定成本为万元，每生产千件，需另投入成本为，当年产量不足千件时，(万元)；当年产量不小于千件时，(万元).通过市场分析，若每件售价为元时，该厂年内生产该商品能全部销售完.

(1)写出年利润(万元)关于年产量(千件)的函数解析式；

(2)年产量为多少千件时，该厂在这一商品的生产中所获利润最大？

18.数列的前项和为，.

(1)若数列成等比数列，求常数的值；

(2)求数列的通项公式；

(3)数列中是否存在三项，它们可以构成等差数列？若存在，请求出一组适合条件的项；若不存在，请说明理由。

17.已知的三边、b、c和面积S满足

16.深圳市的一种特色水果上市时间仅能持续5个月，预测上市初期和后期会因供不应求使价格呈连续上涨态势，而中期又将出现供大于求使价格连续下跌，现有三种价格模拟函数.① 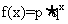;②;③ .

　 (以上三式中均为常数，且，表示4月1日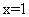，表示5月1日，依次类推).

　 (1)为准确研究其价格走势，应选_______种价格模拟函数.

　 (2)若，，预测该果品在_________月份内价格下跌.

15.若角终边落在射线上，则________.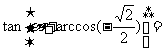

14.如图，函数的图象在点P处的切线方程是

　　 ，则=　　　　 .