
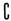 1.设全集
1.设全集 UA={5,7},则a的值为 ( )
UA={5,7},则a的值为 ( )
A.2 B.8 C.-2或8 D.2或8
2.(文)已知函数 时有最大值,则θ的一个值是( )
时有最大值,则θ的一个值是( )
A.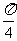 B.
B.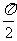 C.
C. D.
D.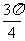
(理)使 为奇函数,且在
为奇函数,且在 上是减函数的
上是减函数的 的一个值是( ) A.
的一个值是( ) A.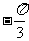 B.
B. C.
C. D.
D.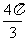
22.(12分)
在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布 。已知成绩在90分以上(含90分)的学生有12名。
。已知成绩在90分以上(含90分)的学生有12名。
(Ⅰ)、试问此次参赛学生总数约为多少人?
(Ⅱ)、若该校计划奖励竞赛成绩排在前50名的学生,试问设奖的分数线约为多少分?
可共查阅的(部分)标准正态分布表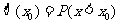
 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1.2 1.3 1.4 1.9 2.0 2.1 |
0.8849 0.9032 0.9192 0.9713 0.9772 0.9821 |
0.8869 0.9049 0.9207 0.9719 0.9778 0.9826 |
0.888 0.9066 0.9222 0.9726 0.9783 0.9830 |
0.8907 0.9082 0.9236 0.9732 0.9788 0.9834 |
0.8925 0.9099 0.9251 0.9738 0.9793 0.9838 |
0.8944 0.9115 0.9265 0.9744 0.9798 0.9842 |
0.8962 0.9131 0.9278 0.9750 0.9803 0.9846 |
0.8980 0.9147 0.9292 0.9756 0.9808 0.9850 |
0.8997 0.9162 0.9306 0.9762 0.9812 0.9854 |
0.9015 0.9177 0.9319 0.9767 0.9817 0.9857 |
21. (12分)已知数列(8×1)/(12×32),(8×2)/(32×52),…,(8×n)/[(2n-1)2×(2n+1)2],…,Sn为其前n项和。计算得S1=8/9,S2=24/25,S3=48/49,S4=80/81,观察上述结果,推测出计算Sn的公式,并用数学归纳法加以证明。
20.(12分)张三开车回家途中有6个交通岗,他在每个路口遇到红灯的事件是相互独立的,并且概率都是
(1)设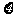 为他在途中遇到的红灯次数,求
为他在途中遇到的红灯次数,求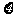 的期望和方差;
的期望和方差;
(2)设 表示他在首次停车前经过的路口数,求
表示他在首次停车前经过的路口数,求 的分布列。
的分布列。
19.
(14分)从5名女生和2名男生中任选3人参加英语演讲比赛,设随机变量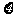 表示所选3人中男生的人数.
表示所选3人中男生的人数.
(1)求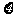 的分布列; (2)求
的分布列; (2)求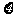 的数学期望;
的数学期望;
(3)求“所选3人中男生人数 ”的概率.
”的概率.
18.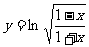 (12分)求下列函数的导数:
(12分)求下列函数的导数:
(1)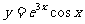 ; (2)
.
; (2)
.
17. (12分)求下列极限:
(1) ;
;
(2) .
.
16.随机变量ξ的概率分布规律为 其中
其中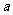 是常数,则
是常数,则  的值为
.
的值为
.
15.某县三个镇共有高中生2000名,且这三个镇高中生人数之比2:3:5,若学生甲被抽到的概率为 ,则这三个镇被抽到的高中生人数分别为________,________,________.
,则这三个镇被抽到的高中生人数分别为________,________,________.
14. 某公司有5万元资金用于投资开发项目,如果成功,一年后可获利10%,一旦失败,一年后将丧失全部资金的50%,下表是过去200例类似项目开发的实施结果:
|
投资成功 |
投资失败 |
|
192次 |
8次 |
则该公司一年后估计可获收益的期望是__________(元).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com