
5.函数y=2-cosx的单调递减区间是 ( )
A.[kπ+π, kπ+2π](k∈Z) B.[2kπ-π, 2kπ](k∈Z)
C.[2kπ,2 kπ+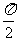 ](k∈Z) D.[2kπ,2kπ+π](k∈Z)
](k∈Z) D.[2kπ,2kπ+π](k∈Z)
4.已知f(x)=ax(a>0,且a≠1),f-1(2)<0,则f-1(x+1)的图象是 ( )

3.已知数列{an}是等比数列,且每一项都是正数,若a2,a48是2x2-7x+6=0的两个根,则
a1·a2·a25·a48·a49的值为 ( )
A. B.9
B.9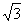 C.±9
C.±9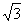 D.35
D.35
2.已知α、β分别表示两个平面,a,b分别表示两条直线,则a//α的一个充分条件是( )
A.α⊥β,a⊥β B.α∩β=b, a//b C.a//b,b//α D.α//β,a β
β
1.已知复数z满足|z|-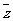 =2+4
=2+4 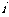 (
(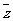 表示复数z的共轭复数),则z等于 ( )
表示复数z的共轭复数),则z等于 ( )
A.3-4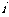 B.3+4
B.3+4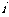 C.-3-4
C.-3-4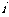 D.-3+4
D.-3+4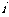
20.(本小题满分14分)
设 ,定点F(a,0),直线l :x=-a交x轴于点H,点B是l上的动点,过点B垂直于l的直线与线段BF的垂直平分线交于点M.
,定点F(a,0),直线l :x=-a交x轴于点H,点B是l上的动点,过点B垂直于l的直线与线段BF的垂直平分线交于点M.
(I)求点M的轨迹C的方程;
(II)设直线BF与曲线C交于P,Q两点,证明:向量 、
、 与
与 的夹角相等.
的夹角相等.
19.(本小题满分13分)
设 函数
函数
(I)求 的反函数
的反函数 ;
;
(II)若 在[0,1]上的最大值与最小值互为相反数,求a的值;
在[0,1]上的最大值与最小值互为相反数,求a的值;
(III)若 的图象不经过第二象限,求a的取值范围.
的图象不经过第二象限,求a的取值范围.
18.(本小题13分)
 如图,ABCD-A1B1C1D1是正四棱柱,则棱长为3,底面边长为2,E是棱BC的中点.
如图,ABCD-A1B1C1D1是正四棱柱,则棱长为3,底面边长为2,E是棱BC的中点.
(I)求异面直线AA1和BD1所成角的大小;
(II)求证:BD1∥平面C1DE;
(III)求二面角C1-DE-C的大小.
17.(本小题13分)
在一天内甲、乙、丙三台设备是否需要维护相互之间没有影响,且甲、乙、丙在一天内不需要维护的概率依次为0.9、0.8、0.85. 则在一天内
(I)三台设备都需要维护的概率是多少?
(II)恰有一台设备需要维护的概率是多少?
(III)至少有一台设备需要维护的概率是多少?
16.(本小题13分)
已知函数
(I)求 的定义域;
的定义域;
(II)求 的值域;
的值域;
(III)设α的锐角,且
 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com