
3.下列命题中是全称命题并且是真命题的是 ( )
A.每个二次函数的图象开口都向上
B.对任意非正数c,若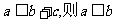
C.存在一条直线与两个相交平面都垂直
D.存在一个实数x使不等式 成立
成立
1.化简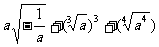 得 ( )
得 ( )
A. B.
B. C.-
C.- D.-
D.- +2a
+2a
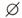
 2.设全集U=R,集合
2.设全集U=R,集合 ,则下列关系正确的是 ( )
,则下列关系正确的是 ( )
A. B.
B. C.
C. D.( M)∩N=
D.( M)∩N=
22.(本小题满分14分)
设数列 的各项都是正数,
的各项都是正数,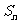 为前n项和,且对任意
为前n项和,且对任意 ,都有
,都有
(1)求证: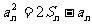 ;
;
(2)求数列 的通项公式;
的通项公式;
(3)若 为非零常数,
为非零常数, ),问是否存在整数
),问是否存在整数 ,使得对任意
,使得对任意 ,都有
,都有
21.(本小题满分12分)
已知AB是抛物线 的任一弦,F为抛物线的焦点,l为准线.m是过点A且以向量
的任一弦,F为抛物线的焦点,l为准线.m是过点A且以向量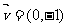 为方向向量的直线.
为方向向量的直线.
(1)若过点A的抛物线的切线与y轴相交于点C,求证:|AF|=|CF|;
(2)若 异于原点),直线OB与m相交于点P,求点P的轨迹方程;
异于原点),直线OB与m相交于点P,求点P的轨迹方程;
(3)若AB过焦点F,分别过A,B的抛物线两切线相交于点T,求证: 且T在直线l上.
且T在直线l上.
|
20.(本小题满分12分)
如图,在梯形ABCD中,AB∥CD∠ADC=90°,3AD=DC=3,AB=2,E是DC上一点,满足DE=1,连接AE,将△DAE沿AE折起到△D1AE的位置,使得∠D1AB=60°,设AC与BE的交点为O.
(I)试用基向量 表示向量
表示向量 ;
;
(II)求异面直线OD1与AE所成角的余弦值;
(III)判断平面D1AE与平面ABCE是否垂直?并说明理由.

19.(本小题满分12分)
已知 的两个根,不等式
的两个根,不等式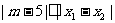 对任意实数
对任意实数 恒成立;Q:函数
恒成立;Q:函数 上有极值. 求使“P且Q”为真命题的m的取值范围.
上有极值. 求使“P且Q”为真命题的m的取值范围.
18.(本小题满分12分)
校文娱队每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人. 设ξ为选出的既会唱歌又会跳舞的人数,且P(ξ>0)=
(I)求文娱队的人数;
(II)写出ξ的概率分布列并计算Eξ.
17.(本小题满分12分)
若函数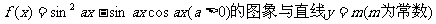 相切,并且切点的横坐标依次成的等差数列,且公差为
相切,并且切点的横坐标依次成的等差数列,且公差为
(I)求m的值;
(II)若点A(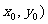 是
是 图象的对称中心,且
图象的对称中心,且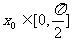 ,求点A的坐标.
,求点A的坐标.
16. 如图,设平面
如图,设平面 =EF,AB⊥α,CD⊥α,垂足分别为B、D. 若增加一个条件,就能推出BD⊥EF.现有:
=EF,AB⊥α,CD⊥α,垂足分别为B、D. 若增加一个条件,就能推出BD⊥EF.现有:
①AC⊥β;
②AC与α,β所成的角相等;
③AC与CD在β内的射影在同一条直线上;
④AC∥EF.
那么上述几个条件中能成为增加条件的是 .(填上你认为正确的答案序号).
15.已知向量 的夹角等于 .
的夹角等于 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com