19.(本小题满分12分)

如图，已知直平行六面体ABCD-A₁B₁C₁D₁中，AD⊥BD，AD= BD =a，AA₁=a，E是CC₁的中点。

(Ⅰ)求证：AD⊥平面BDE；　　　　　　　　　　　　　　　　　　　　

(Ⅱ)求点D₁到平面BDE的距离；

(Ⅲ)求二面角B-DE-C的大小。

18.(本小题满分12分)

　　 有红蓝两粒质地均匀的正方体形状的骰子，红色骰子有两个面是8点，四个面是2点，蓝色骰子有三个面是7点，三个面是1点，两人各取一只骰子分别随机投掷一次，所得点数较大者获胜。

　　 (Ⅰ)分别求出投掷两只骰子所得点数的分布列及期望；

(Ⅱ)投掷红色骰子者获胜的概率是多少?

17.(本小题满分12分)

已知向量a=(sinx，cosx)，b=(cosx，cosx)，c=(2，1)，

(Ⅰ)若a∥c，求sinxcosx的值；

(Ⅱ)若0<x≤，求函数f(x)=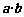的值域。

16.为激发学生学习的兴趣，老师上课时在黑板上写出三个集合：A={<0}，B=

{}，C={>1}；然后叫甲、乙、丙三位同学到讲台上，并将“”中的数告诉了他们，要求他们各用一句话来描述，以便同学们能确定该数。以下是甲、乙、丙三位同学的描述：

　 甲：此数为小于6的正整数，

　 乙：A是B成立的充分不必要条件，

　 丙：A是C成立的必要不充分条件。

若老师评说三位同学都说得对，则“”中的数为　　　　　　 。

15.为了了解“预防禽流感疫苗”的使用情况，某市卫生部门对本地区9月份至11月份使用疫苗的所有养鸡场进行了调查，根据下列图表提供的信息，可以得出这三个月每月注射了疫苗的鸡的数量平均为　　　 万只。

14.曲线y=cosx(0≤x≤)与坐标轴所围成图形的面积是　　　　　　 。

13.若复数 (b∈R)的实部与虚部互为相反数，则b=　　　　 。

10.2006年世界帆船比赛期间，我市某高校有14名志愿者参加接待工作，若每天早、中、晚三班每班4人，每人每天最多值一班，则开幕式当天不同的排班种数为

　 (A)　　 (B)　　 (C)　　 (D)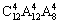

(11)函数f(x) =Asin(ωx+)(A>0，ω>0)的部分图象如图所示，

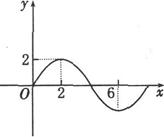
　 则，f(1) + f(2)+ f(3)+…+ f(2007)的值为

　 (A)0　　　 (B)　　 (C)2+　　 (D)2-

(12)关于x的实系数方程x²-ax+2b=0的一根在区间[0，1]上，

　 另一根在区间[1，2]上，则2a+3b的最大值为

　 (A)3　　 　　(B)5　　 　　(C)8　 　　　　(D)9

第Ⅱ卷(非选择题，共90分)

9.用数学归纳法证明1+2+3+…+n²=，则当n=k+1时左端应在n=k的基础上加上

　 (A)k²+1　　　　　　　　　　　　 (B)(k+1)²

　 (C)　　　　　　 (D)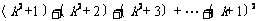

8.已知点P是圆C：x²+y²+4x+ay-5=0上任意一点，P点关于直线2x+y-1=0的对称点也在圆C上，则实数a的值是

　 (A)10　 　　　　　(B)12　 　　　　　　(C)-10　 　　　　　　(D)-12