7．在各项都是正数的等比数列{a_n}中，首项a₁=2，前3项和为14，则a₄+a₅+a₆的值为

　(A)52　　　　　　 　(B)56　　　　　　 　(C)112　　　　　　 　(D)378

6．一质点运动时速度与时间的关系为V(t)=t²-t+2，质点作直线运动，则此物体在[1，2]时间内的位移为

　(A)　　　　 　　(B)　　　　 　　(C)　　　　　 　　(D)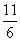

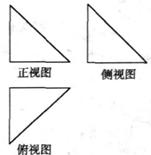
5．如图，一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形，且直角边长为1，那么这个几何体的体积为

　(A)l　　　　　　　　 (B)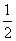　　

　(C)　　　　　　 　(D)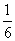

4．设直线过点(a，0)，其斜率为-1，且与圆x²+y²=2相切，则a的值为

(A)±　　　 　　(B)±2　　　　　　　　

(C)±2　　　 　　(D)±4

3．下列函数中周期为2的函数是

　(A)y=2cos² x-1　　　　　　　　　　　　　　 　(B)y=sin²x+cos2x

　(C)y=ta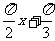n()　　　　　　　　　　　　 　(D)y=sinxcosx

2．命题“三角形中最多有一个内角是钝角”的否定是

　(A)有两个内角是钝角　　　　　　　　　　　　 　(B)有三个内角是钝角

　(C)至少有两个内角是钝角　　　　　　　　　　 (D)没有一个内角是钝角

1．

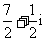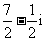　(A)　　　　 　　(B)　　　　 　　(C)　　　 　　(D)

　　 (17)(本小题满分12分)

　　 已知函数．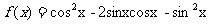

　　 (I)在给定的坐标系中，作出函数在区间[]上的图象；

　　 (Ⅱ)求函数在区间[]上的最大值和最小值

(18)(本小题满分12分)

已知函数，，成等比数列．设(n∈N^*)，求数列{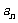}的前n项和．

(19)(本小题满分12分)

如图，在正方体ABCD-A₁B₁C₁D₁中，E、F、M分别是棱B₁C₁、B₁B、C₁D₁的中点．

　　 (I)求证：CF⊥平面EAB；

　　 (Ⅱ)是否存在过E、M点且与平面A₁FC平行的平面?若存在，请指出并证明之；若不存在，请说明理由．

(20)(本小题满分12分)

市政府为招商引资，决定对外资企业第一年产品免税．某外资厂该年A型产品出厂价为

每件60元，年销售量为11．8万件．第二年，当地政府开始对该商品征收税率为p%(0<p<

100，即销售100元要征收p元)的税收，于是该产品的出厂价上升为每件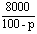元，预计年销售量将减少p万件．

　　 (I)将第二年政府对该商品征收的税收y(万元)表示成p的函数，并指出这个函数的定

义域；

　　 (Ⅱ)要使第二年该厂的税收不少于16万元，则税率p%的范围是多少?

　　 (Ⅲ)在第二年该厂的税收不少于16万元的前提下，要让厂家获得最大销售金额，则p应为多少?

(21)(本小题满分12分)

　　 已知椭圆的上、下顶点分别是A、B，点M是椭圆上的动点(不与A、B重合)，直线AM交直线y=2于点N，且BM⊥BN

　　 (I)求椭圆的方程；

　　 (Ⅱ)若斜率为1的直线l交椭圆于P、Q两点，求证：OP+OQ与向量a=(-3，1)共线(其

中O为坐标原点)．

　　 (22)(本小题满分14分)

在实数集R上定义运算：xy=x(a-y)(a∈R，a为常数)．若，,

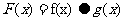
(I)求F(x)的解析式；

　　 (Ⅱ)若F(x)在R上是减函数，求实数a的取值范围；

　　 (Ⅲ)若a=-3，在F(x)的曲线上是否存在两点，使得过这两点的切线互相垂直?若存在，求出切线方程；若不存在，说明理由．

16．加工火腿肠的主要原料是精肉和面粉．若A、B两种火腿肠的精肉和面粉的搭配如下表，且A、B的价格分别为0．6元／支、0．8元／支．现有精肉2吨，面粉2．5吨，用以加工A、B两种火腿肠．假设产品供不应求，那么可以获得的最大销售额为_______

原料 产品	精肉(千克)	面粉(千克)
A(千支)	20	30
B(千支)	30	20

14．在公差为d(d≠O)的等差数列{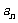}中，若是{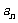}的前n项和，则数列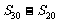，，也成等差数列，且公差为100d．类比上述结论，在公比为q(q≠1)的等比数列{}中，若是数列{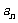}的前n项之积，则有______________

　　 15．已知点B(1，0)，点0为坐标原点，点A在圆上，则向量OA与OB的夹角的最大值与最小值分别为_________