20.(本小题满分12分)

　　 在直三棱柱ABC-A₁B₁C₁中，A₁A=AB=2，AC=BC，E为B₁C上一点，且BE⊥平面ACB₁，

　(Ⅰ)求证：AC⊥平面BB₁C₁C；

　(Ⅱ)求二面角B-AB₁-C的大小；

　(Ⅲ)求点A₁到平面ACB₁的距离.

19.(本小题满分12分)

　　 公差为正数的等差数列{a_n}的前n项和为S_n，且S_n=()²，n∈N*.

　(Ⅰ)求数列{a_n}的通项公式；

　(Ⅱ) 设数列{a_n}中的部分项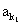，，，…，…恰成等比数列，其中k₁=2，k₃=14，求k₁+k₂+…+k_n的值；

　(Ⅲ)设b_n=记T_n=b₁+b₂+…+b_n，问是否存在某个无限集M，当n∈M时，都有|T_n-|<成立？若存在，请找出一个这样的集合M；若不存在，请说明理由.

18.(本小题满分12分)

　　 甲、乙两人进行羽毛球比赛，在每一局比赛中，甲获胜的概率都是P.

(Ⅰ)如果甲、乙两人比赛5局，甲恰好胜3局的概率不小于恰好负3局概率，试求P的取值范围；

(Ⅱ)如果甲乙两人比赛8局，则甲恰好胜4局的概率有可能是吗？为什么？

17.(本小题满分12分)

知函数f(x)=a+bsin2x+ccos2x的图象经过点A(0，1)的图象经过点A(0，1)，B(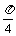，1)时，且当x∈[0, 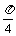]时，f(x)取得最大值2

(Ⅰ)求f(x)的解析式；

(Ⅱ)是否存在向量m，使得将f(x)的图象按向量m平移后可以得到一个奇函数的图象？若存在，求出满足条件的一个m；若不存在，说明理由.

16.设f(x)=若f(k)>k，则实数k的取值范围是_________.

15.某篮球队的12名队员(含2外援)中有5名主力队员(含一名外援)，主教练要从12名队员中选5人首发上场，则主力队员不少于4人，且有一名外援上场的概率是_________.

14.Rt△ABC的斜边AB在平面α内，∠CAB=30°，若直角边BC与平面α所成角的正弦值为则AC与平面α所成角的大小为___________。

13.设等比数列{a_n}的公比为q，前n项和为S_n，若S_n+1，S_n，S_n+2成等差数列，则q的值为_________.

12.对于直角坐标系内任意两点P₁(x₁，y₁),P(x₂，y₂)，定义运算P₁×P₂=(x₁,y₁)×(x₂，y₂)=(x₁,x₂)=

(x₁x₂-y₁y₂,x₁y₂+x₂y₁)，若M是与原点相异的点，且M×(1，1)=N，则∠MON=

　A.　　　　　　 B.　　　　　　　　 C.　　　　　　　　 D.

11.已知关于x的二次方程x²+(m+2)x+m+n+1=0的两根为x₁，x₂，且0<x₁<1<x₂，则的取值范围是

　A.(-∞，-2)　　　　　　 B.(-2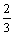，-)　　　　 C.(-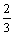，0)　　　　　 D.(0，+∞)