
6.下面是高考第一批录取的一份志愿表。现有4所重点院校,每所院校有3 个专业是你较为满意的选择,如果表格填满且规定学校没有重复,同一学校的专业也没有重复的话,你将有( )种不同的填写方法.
志 愿 学 校 专 业
第一志愿 1 第1专业 第2专业
第二志愿 2 第1专业 第2专业
第三志愿 3
第1专业 第2专业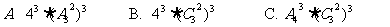

5.已知函数 ,则这一函数的一个递减区间是
,则这一函数的一个递减区间是
A.( ) B.(
) B.( ) C.(
) C.( ) D.(
) D.( )
)
4.已知函数 ,则
,则 的值是( )
的值是( )
A.2 B.-3 C.-2 D.3
3.老师为研究男女同学数学学习的差异情况,对全班50名同学(其中男同学30名,女同学20名),采用分层抽样的方法抽取一个样本容量为10的样本进行研究,某女同学甲被抽取的概率为
A.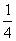 B.
B. C.
C.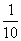 D.
D.
2.定义在R上的函数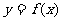 的值域为
的值域为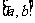 ,则函数
,则函数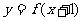 的值域为
的值域为
A.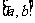 B.
B.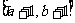 C.
C. D.无法确定
D.无法确定
1.若集合 ,
, ,则“
,则“ ”是“
”是“ ”的
”的
A.充分不必要条件. B. 必要不充分条件.
C.充要条件. D. 既不充分也不必要条件.
22.(本小题满分14分)
已知函数f(x)=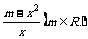
(Ⅰ)设g(x)=f(x)+lnx,当m≥-2时,求g(x)在[ ]上的最大值;
]上的最大值;
(Ⅱ)若y=log [8-f(x)]在[1,+∞]上是单调减函数,求实数m的取值范围.
[8-f(x)]在[1,+∞]上是单调减函数,求实数m的取值范围.
21.(本小题满分12分)
已知双曲线C: 的离心率为
的离心率为 ,右焦点为F,过点M(1,0)且斜率为1的直线与双曲线C交于A、B两点,并且
,右焦点为F,过点M(1,0)且斜率为1的直线与双曲线C交于A、B两点,并且
(Ⅰ)求双曲线C的方程;
(Ⅱ)过右焦点F作直线l,交双曲线C的右支于P、Q两点,问在原点和右顶点之间是否存在点N,使得无论直线l的倾斜角多大,都有∠PNF=∠QNF?若存在,试确定点N的位置;若不存在,说明理由.
20.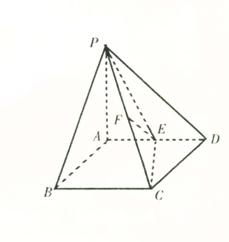 (本小题满分12分)
(本小题满分12分)
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E、F分别为棱AD、PC的中点.
(Ⅰ)求异面直线EF和PB所成角的大小;
(Ⅱ)求证:平面PCE⊥平面PBC;
(Ⅲ)求二面角E-PC-D的大小.
19.(本小题满分12分)
从原点出发的某质点M,按向量a =
(0,1) 移动的概率为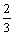 ,按向量b =
(0,2) 移动的概率为
,按向量b =
(0,2) 移动的概率为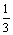 ,设M可到达点(0,n)的概率为Pn.
,设M可到达点(0,n)的概率为Pn.
(Ⅰ)求P1和P2的值;
(Ⅱ)设bn=Pn+1-Pn,求证数列{bn}是等比数列;
(Ⅲ)求数列{Pn}的通项公式及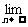 Pn.
Pn.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com