
20. (本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分4分,第3小题满分8分.
 通常用
通常用 分别表示△
分别表示△ 的三个内角
的三个内角 所对边的边长,
所对边的边长,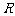 表示△
表示△ 的外接圆半径.
的外接圆半径.
(1) 如图,在以 为圆心、半径为2的⊙
为圆心、半径为2的⊙ 中,
中,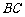 和
和
 是⊙
是⊙ 的弦,其中
的弦,其中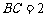 ,
, ,求弦
,求弦 的长;
的长;
(2) 在△ 中,若
中,若 是钝角,求证:
是钝角,求证: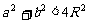 ;
;
(3) 给定三个正实数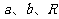 ,其中
,其中 . 问:
. 问: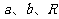
满足怎样的关系时,以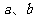 为边长,
为边长,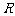 为外接圆半径的△
为外接圆半径的△ 不存在、存在一个或存在两个(全等的三角形算作同一个)?在△
不存在、存在一个或存在两个(全等的三角形算作同一个)?在△ 存在的情况下,用
存在的情况下,用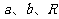 表示
表示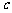 .
.
[解] (1)
(2)
(3)
19. (本题满分14分)本题共有2个小题,第1小题满分4分,第2小题满分10分.
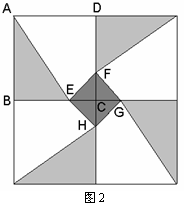 某人定制了一批地砖. 每块地砖 (如图1所示)是边长为
某人定制了一批地砖. 每块地砖 (如图1所示)是边长为 米的正方形
米的正方形 ,点E、F分别在边BC和CD上, △
,点E、F分别在边BC和CD上, △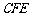 、△
、△ 和四边形
和四边形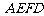 均由单一材料制成,制成△
均由单一材料制成,制成△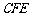 、△
、△ 和四边形
和四边形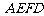 的三种材料的每平方米价格之比依次为3:2:1. 若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形
的三种材料的每平方米价格之比依次为3:2:1. 若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形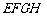 .
.
(1) 求证:四边形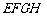 是正方形;
是正方形;
(2)  在什么位置时,定制这批地砖所需的材料费用最省?
在什么位置时,定制这批地砖所需的材料费用最省?
[解] (1)
(2)
18. (本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
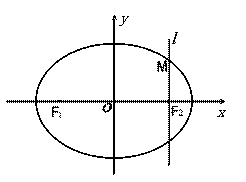 如图,在直角坐标系
如图,在直角坐标系 中,设椭圆
中,设椭圆
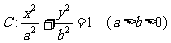 的左右两个焦点
的左右两个焦点
分别为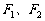 . 过右焦点
. 过右焦点 且与
且与 轴垂直的直线
轴垂直的直线 与椭圆
与椭圆 相交,其中一个交点为
相交,其中一个交点为 .
.
(1) 求椭圆 的方程;
的方程;
(2) 设椭圆 的一个顶点为
的一个顶点为 ,直线
,直线 交椭圆
交椭圆 于另一点
于另一点 ,求△
,求△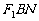 的面积.
的面积.
[解] (1)
(2)
17. (本题满分14分)
求出一个数学问题的正确结论后,将其作为条件之一,提出与原来问题有关的新问题,我们把它称为原来问题的一个“逆向”问题.
例如,原来问题是“若正四棱锥底面边长为4,侧棱长为3,求该正四棱锥的体积”.求出体积 后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为
后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为 ,求侧棱长”;也可以是“若正四棱锥的体积为
,求侧棱长”;也可以是“若正四棱锥的体积为 ,求所有侧面面积之和的最小值”.
,求所有侧面面积之和的最小值”.
试给出问题“在平面直角坐标系 中,求点
中,求点 到直线
到直线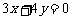 的距离.”的一个有意义的“逆向”问题,并解答你所给出的“逆向”问题.
的距离.”的一个有意义的“逆向”问题,并解答你所给出的“逆向”问题.
[解]
16. (本题满分12分)
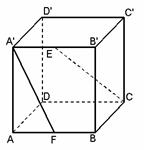 如图,在棱长为2的正方体
如图,在棱长为2的正方体 中,
中, 分别是
分别是 和
和 的中点,求异面直线
的中点,求异面直线 与
与 所成角的大小 (结果用反三角函数值表示).
所成角的大小 (结果用反三角函数值表示).
[解]
15.设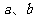 是正实数,以下不等式
是正实数,以下不等式
①  ,②
,② 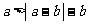 ,③
,③ 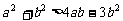 ,④
,④ 
恒成立的序号为
(A) ①、③. (B) ①、④. (C) ②、③. (D) ②、④. [答] ( )
14. 下列四个函数中,图像如图所示的只能是
下列四个函数中,图像如图所示的只能是
(A)  .
(B)
.
(B)  .
.
(C) 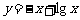 .
(D)
.
(D)  .
.
[答] ( )
13.如图,平面内的两条相交直线 和
和 将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ (不
将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ (不
包括边界). 若 ,且点
,且点 落在第Ⅲ部分,则实数
落在第Ⅲ部分,则实数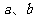 满足
满足
 (A)
(A) 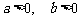 . (B)
. (B)  .
.
(C) 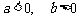 .
(D)
.
(D)  .
.
[答] ( )
12.若集合 ,
, ,则“
,则“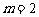 ”是“
”是“ ”的
”的
(A) 充分不必要条件. (B) 必要不充分条件.
(C) 充要条件. (D) 既不充分也不必要条件. [答] ( )
11.函数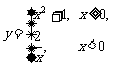 的反函数是
.
的反函数是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com