4． 在底面是矩形的直四棱柱ABCD-A₁B₁C₁D₁中，∠DAD₁=∠CDC₁=45°，那么异面直线AD₁与DC₁所成角的度数为

(A)　 30°　　 (B)　 45°　　 (C)　 60°　　 (D)　 90°

3． 把编号为1、2、3、4的4位运动员排在编号为1、2、3、4的4条跑道中，要求有且只有两位运动员的编号与其所在跑道的编号相同，共有不同的排法种数是

(A) 3　　　　　　　 (B) 6 　　　　　　(C) 12　　　　　　　　 (D) 24

2．已知等差数列{a_n}中，a₆+a₁₀=16，a₄=1，则a₁₂的值是

(A) 15　　　　　　　 (B) 30　　　　　　　 (C) 31　　　　　　　 (D) 64

题后括号内．

1．已知集合M={y|y=2^x,xÎR},P={y|y=}，则MÇP是

(A) {y|y>1}　　　 　(B) {y|y³1}　　　　　 (C) {y|y>0}　　　　　 (D) Æ

20．(13分)已知双曲线的中心在原点，以两条坐标轴为对称轴，离心率是，两准线间的距离大于，且双曲线上动点P到A(2，0)的最近距离为1。

(Ⅰ)求证：该双曲线的焦点不在y轴上；

(Ⅱ)求双曲线的方程；

(Ⅲ)如果斜率为k的直线L过点M(0，3)，与该双曲线交于A、B两点，若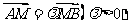，试用l表示k²,并求当时，k的取值范围。

19．(14分)已知函数f(x)=.

(Ⅰ)求函数f(x)在区间[1,e]上的最大值、最小值；

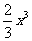(Ⅱ)求证：在区间(1,上函数f(x)的图像在函数g(x)=图像的下方；

(Ⅲ)请你构造函数(x)，使函数F(x)=f(x)+(x)在定义域(0,上，存在两个极值点，并证明你的结论.

18．(14分)已知各项均为正数的数列{}满足，且是的等差中项.

(Ⅰ)求数列{}的通项公式；

(Ⅱ)若=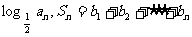，求使S>50成立的正整数n的最小值.

17．(14分)已知四棱锥S--ABCD的底面ABCD是正方形，SA底面ABCD，点E是SC上任意一点.

(Ⅰ)求证：平面EBD平面SAC；

(Ⅱ)设SA=4，AB=2，求点A到平面SBD的距离；

(Ⅲ)当的值为多少时，二面角B-SC-D的大小为120°。

16．(12分)下表为某体育训练队跳高与跳远成绩的统计表，全队有队员40人，成绩分为1分至5分五个档次，例如表中所示：跳高成绩为4分的人数是：1+0+2+5+1=9人；跳远成绩为2分的人数是：0+5+4+0+1=10人；跳高成绩为4分且跳远成绩为2分的队员为5人.

将记载着跳高、跳远成绩的全部队员的姓名卡40张混合在一起，任取一张，记该卡片队员的跳高成绩为x，跳远成绩为y，设x，y为随机变量(注：没有相同姓名的队员)

　　 (1)求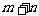的值；

(2)求的概率及且的概率；

(3)若y的数学期望为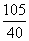，求m，n的值.

15．(13分)已知向量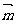=(sin,2cos)，=()

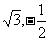(Ⅰ)当qÎ[0，p]时，求函数f()=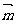×的值域；

(Ⅱ)若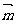∥，求sin2的值.