1．若集合那么　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．M∩N=M　　　　　　 B．M N　　　　　　　 C．N　　 M　　　　 D．M∪N=N

20．(本小题满分14分)

　　　 设定义在R上的函数满足：①对任意的实数R，有；

②

　 (1)求；

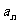　 (2)若在R上为单调递增函数，求数列的通项的表达式.

19．(本题满分13分)

　　　 点A，B分别是以双曲线的焦点为顶点，顶点为焦点的椭圆C长轴的左、右端点，点F是椭圆的右焦点，点P在椭圆C上，且位于x轴上方，.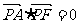

　 (1)求椭圆C的方程；

　 (2)求点P的坐标；

　 (3)设M是椭圆长轴AB上的一点，M到直线AP的距离等于|MB|，求椭圆上的点到点M的距离d的最小值.

18．(本题满分13分)

　　　 某校田径队有三名短跑运动员，根据平时的训练情况统计，甲、乙、丙三人100米跑(互

不影响)的成绩在13秒内(称为合格)的概率分别是.如果对这3名短跑运动员的

100米跑的成绩进行一次检测. 问：

　 (1)三人都合格的概率与三人都不合格的概率分别是多少？

　 (2)出现几个合格的概率最大？

17．(本题满分14分)

　　　 如图：四棱锥P-ABCD底面为一直角梯形，

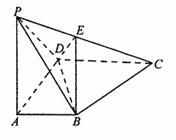， 　 E是PC中点.

　 (1)求证：平面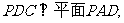

　 (2)求证：

　 (3)假定

的平面角的正切值.

16．(本题满分14分)

　　　 已知R，函数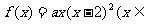R)有极大值32.

　 (1)求实数a的值；

　 (2)求函数的单调区间.

15．(本题满分13分)

　　　 已知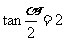，求：

　 (1)的值；

　 (2)的值.

14．抛物线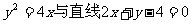交于两点A、B，设抛物线的焦点为F，则|FA|+|FB|=

　　 　　　　　.

13．设二项式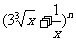的展开式的各项系数的和为P，所有二项式系数的和为S，若P+S=

　　　 272，则n=　　　　　 ,其展开式中的常数项为　　　　　 .

12．已知x、y满足约束条件的最小值为－6，则常数k=　　　　　 .