
(17)(本小题满分12分)
已知 R.
R.
(I)函数 的图象可由
的图象可由 的图象经过怎样的变换得到;
的图象经过怎样的变换得到;
(Ⅱ)设函数 的图象位于y轴右侧的对称中心从左到右依次
的图象位于y轴右侧的对称中心从左到右依次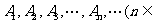 N*),试求
N*),试求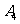 的坐标.
的坐标.
(18)(12分)
在甲袋中有10个螺母,其中9个正品,1个次品;乙袋中有10个螺帽,其中8个正品,2个次品,现要抽取一套正品螺栓(即正品螺母、正品螺帽各一个),若随机不放回地抽取,先定螺母,后定螺帽.
(I)求总共抽取的次数恰好为3的概率;
(Ⅱ)总共抽取次数不超过4的概率。
(19)(12分)
如图,已知正方形ABCD和矩形ACEF所在平面互相垂直, 是线段EF的中点.
是线段EF的中点.

(I)求证:AM 平面BDF;
平面BDF;
(Ⅱ)求证: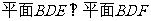 。
。
(20)(12分)
椭圆 与双曲线
与双曲线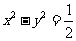 的离心率互为倒数,左焦点
的离心率互为倒数,左焦点 到直线
到直线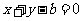 的距离为
的距离为 。
。
(Ⅰ)求椭圆M的方程。
(Ⅱ)若直线l与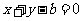 垂直,且与椭圆M有且仅有一个公共点,求直线l的方程。
垂直,且与椭圆M有且仅有一个公共点,求直线l的方程。
(21)(12分)
已知 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且 .若
.若 时,有
时,有 .
.
(I)证明: 在[-1,1]上是增函数;
在[-1,1]上是增函数;
(Ⅱ)解不等式 .
.
(22)(14分)
已知等差数列 ,公差d>0,前n项和为
,公差d>0,前n项和为 .
.
(I)求 的通项公式;
的通项公式;
(Ⅱ)令 ,若
,若 是等差数列,求非零常数c;
是等差数列,求非零常数c;
(Ⅲ)求 N*)的最大值.
N*)的最大值.
(13)复数z满足(1+2i)z=4+3i,那么|z|=
(14)已知a、b都是非零向量,且a+3b与7a-5b垂直,a-4b与7a-2b垂直,则a与b的夹角是 .
(15)已知函数 ,那么
,那么 .
.
(16)若点P在 上,
上,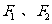 是椭圆的左、右焦点,且
是椭圆的左、右焦点,且 ,则
,则 的面积是
.
的面积是
.
(1)在100个零件中,有一级品20个,二级品30个,三级品50个,从中抽取容量为20的样本。
①采用随机抽样法,将零件编号为00,01,02,…,99,抽取容量为20的样本;
②采用系统抽样法,将所有零件分成20组,每组5个,然后在每组中随机抽取1个;
③采用分层抽样法,从一级品中随机抽取4个,从二级品中随机抽取6个,从三级品中随机抽取10个.
对于上述问题中,下面说法正确的是
(A)不论采用哪一种抽样方法,这100个零件中每个零件被抽到的概率都是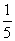
(B)①②两种抽样法,这100个零件中,每个被抽到的概率是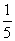 ,③并非如此
,③并非如此
(C)①③两种抽法,这100个零件中,每一个被抽到的概率是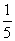 ,②并非如此
,②并非如此
(D)采用不同的抽样方法,这100个零件中,每一个零件被抽到的概率各不相同
(2)不等式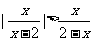 的解集是
的解集是
(A)(0,2)
(B)
(C)( )
(D)
)
(D)
(3)已知条件p:x+y≠-2,条件q:x≠-1或y≠-1,则p是q的
(A)充分非必要条件 (B)必要非充分条件
(C)充要条件 (D)既不充分也不必要条件
(4)已知双曲线中心在原点,且一个焦点为F( ,0),直线y=x-1与其相交于M、N两点,线段MN的中点横坐标为
,0),直线y=x-1与其相交于M、N两点,线段MN的中点横坐标为 ,则此双曲线方程是
,则此双曲线方程是
(A) (B)
(B)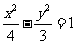 (C)
(C) (D)
(D)
(5)若平面 ,则下列命题中的假命题为
,则下列命题中的假命题为
(A)过点P垂直于平面 的直线平行于平面
的直线平行于平面
(B)过点P在 内作垂直于l的直线垂直于平面
内作垂直于l的直线垂直于平面
(C)过点P垂直于平面 的直线在平面
的直线在平面 内
内
(D)过点P垂直于直线l的直线在平面 内
内
(6)设全集U=R,集合 为常数},且
为常数},且 ,则M与P满足
,则M与P满足
(A)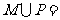 R
(B)
R
(B)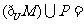 R
R
(C)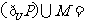 R
(D)
R
(D) R
R
(7)若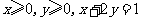 ,那么
,那么 的最小值为
的最小值为
(A)2
(B) (C)
(C) (D)4
(D)4
(8)如图,小圆圈表示网络的结点,结点之间的连线表示它们有网络相联,连线标注的数字表示该线段网线单位时间内,可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为
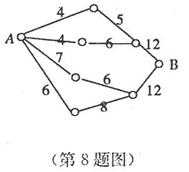
(A)26 (B)24 (C)20 (D)19
(9)如果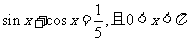 ,那么
,那么 的值为
的值为
(A) (B)
(B) 或
或 (C)
(C) (D)
(D)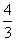 或
或
(10)若a>0使不等式|x-4|+|x-3|<a在R上的解集不是空集,则a的取值范围是
(A)(0,1) (B)(0,1] (C)(1,+∞) (D)[1,+∞)
(11)已知点A(-2,3),B(3,2),直线ax+y+2=0与线段AB有交点,则a的取值范围是
(A)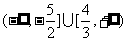 (B)
(B)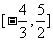
(C)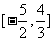 (D)
(D)
(12)函数 有
有
(A)极小值-1,极大值1 (B)极小值-1,极大值3
(C)极小值-2,极大值2 (D)极小值-2,极大值3
第Ⅱ卷 (非选择题 共90分)
22.(本小题12分)
已知定点 ,动点B是圆F:
,动点B是圆F: (F为圆心)上一点,线段AB的垂直平分线交BF与P。
(F为圆心)上一点,线段AB的垂直平分线交BF与P。
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)直线 交P点的轨迹于M、N两点,若P点的轨迹上存在点C,使
交P点的轨迹于M、N两点,若P点的轨迹上存在点C,使
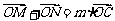 ,求实数m的值;
,求实数m的值;
(Ⅲ)是否存在过点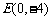 的直线l交P点的轨迹于点R、T,且满足
的直线l交P点的轨迹于点R、T,且满足 (O为原点)?若存在,求直线l的方程,若不存在,请说明理由。
(O为原点)?若存在,求直线l的方程,若不存在,请说明理由。
21.(本小题12分)
对于函数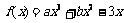 ,
,
(Ⅰ)若 在x=1和x=3处取得极值,且
在x=1和x=3处取得极值,且 的图像上每一点的切线的斜率均不超过
的图像上每一点的切线的斜率均不超过
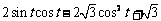 ,试求实数t的取值范围;
,试求实数t的取值范围;
(Ⅱ)若 为实数集R上的单调函数,且
为实数集R上的单调函数,且 ,设P点的坐标为
,设P点的坐标为 ,试求出点P的轨迹所形成的图形的面积S。
,试求出点P的轨迹所形成的图形的面积S。
20.(本小题12分)
已知函数 的图像经过坐标原点,且
的图像经过坐标原点,且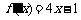 ,数列{an}的前n项和
,数列{an}的前n项和
 ,{bn}为等比数列,且
,{bn}为等比数列,且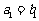 ,
, 。
。
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)记 ,是否存在正整数M,使得对一切
,是否存在正整数M,使得对一切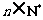 ,
, 都成立?
都成立?
若存在请求出M的最小值;若不存在,请说明理由。
19.(本小题12分)
某公厂统计资料显示,产品次p品率与日产量x(单位件,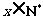 ,
, )的关系如下:
)的关系如下:
|
x |
1 |
2 |
3 |
4 |
… |
96 |
|
p |
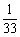 |
 |
 |
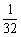 |
… |
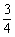 |
又知每生产一件正品盈利a(a为正常数)元,每生产一件次品就损失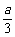 元。
元。
(Ⅰ)将该厂日盈利额T(元)表示为日产量x的函数;
(Ⅱ)为了获得最大盈利,该厂的日产量应定为多少件?
( )
)
18.(本小题12分)
 四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,且PA=AD=2AB,点M、N分别在侧棱PD、PC上,且
四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,且PA=AD=2AB,点M、N分别在侧棱PD、PC上,且
(Ⅰ)求证:平面AMN⊥平面PCD;
(Ⅱ)若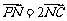 ,求平面AMN与
,求平面AMN与
平面PAB所成二面角的余弦值。
17.(本小题12分)
在 中,设内角A、B、C的对边分别为a、b、c,向量
中,设内角A、B、C的对边分别为a、b、c,向量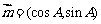 ,向量
,向量
 ,若
,若
(Ⅰ)求角A的大小;
(Ⅱ)若 ,且
,且 ,求
,求 的面积。
的面积。
16.给出四个命题:
①若 ,则
,则 ;
;
②函数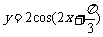 的图像关于点
的图像关于点 对称;
对称;
③函数 是周期函数,且周期为
是周期函数,且周期为
④函数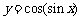
 为偶函数,其中所有正确的序号是
。
为偶函数,其中所有正确的序号是
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com