3．函数y=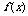是定义在(－2，2)上的奇函数，当x∈(0，2)时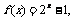，则的值为　　　　 　　　　　　　　　 (　　 )

　　 A．－1　　　　　　 B．　　　　　　 C．7　　　　　　　 D．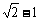

2．若不等式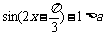对于任意的实数x都成立，则实数a的取值范围是(　　 )

　　 A．(－2，+∞)　　 B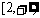．　　　　 C．　　　　 D．(－∞，－2)

1．设集合　　　　　　 (　　 )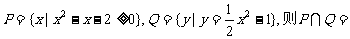

　　 A．{m|－1≤m＜2}　　　　　　　　　　 B．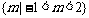

　　 C．　　　　　　　　　　　　　　　　　 D．{－1}

20．(本小题共14分)

　　　　 已知函数图象上的两点，横坐标为的点P满足(O为坐标原点).

　 (Ⅰ)求证：为定值；

　 (Ⅱ)若；

　 (Ⅲ)已知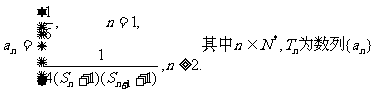的前n项和，若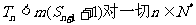都成立，试求m的取值范围.

19．(本小题共13分)

已知双曲线的右焦点是F，右顶点是A，虚轴的上端点是B，且

　 (Ⅰ)求双曲线C的方程；

　 (Ⅱ)过点P(0,4)的直线l，交双曲线C于M、N两点，交x轴于点Q(点Q与双曲线C 的顶点不重合)，当时，求点Q的坐标.

18．(本小题共13分)

某学生玩投飞镖游戏，他一次投镖所得环数m的概率分布如下：

若这名学生投两次飞镖，记两次投中的最高环数为ξ.

　 (Ⅰ)求该名学生两次都投中8环的概率；

　 (Ⅱ)求ξ的分布列和数学期望Eξ.

17．(本小题共14分)

　 如图，在四棱锥P-ABCD中，底面ABCD为正方形，PD⊥平面ABCD，且PA=AB=2，E是PB的中点，F是AD的中点.

　 (Ⅰ)求异面直线PD一AE所成角的大小；

　 (Ⅱ)求证：EF平面PBC；

　 (Ⅲ)求二面角F-PC-B的大小.

16．(本小题共13分)

　 已知△ABC的三个内角分别为A，B，C，向量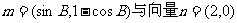 夹角的余弦角为

　 (Ⅰ)求角B的大小；

　 (Ⅱ)求的取值范围.

15．(本小题共13分)

设函数相切于点A，且点A的横坐标为1.

　 (Ⅰ)求a，b的值；

　 (Ⅱ)求函数f(x)的单调区间，并指出在每个区间上的增减性.

14．定义一种运算“*”，它对于整数n满足以下运算性质：

　 (1)2*1001=1；(2)(2n+2)*1001=3·[(2n)*1001]，则2008*1001的值是　　 　　.