
8.(理)设直线过点(0,a),其斜率为1,且与圆x2+y2=2相切,则a的值为( )
A.±4
B.±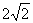 C.±2
D.±
C.±2
D.±
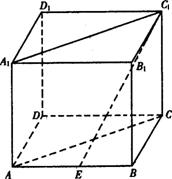
(文)正方体ABCD-A1B1C1D1中,若E为棱AB的中点,则直线C1E与平面ACC1A1所成角的正切值为( )
A.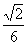 B.
B. C.
C. D.
D.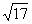
7.(理)正方体ABCD-A1B1C1D1中,若E为棱AB的中点,则直线C1E与平面ACC1A1所成角的正切值为( )

A.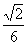 B.
B. C.
C. D.
D.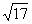
(文)设m,n是两条不同的直线,α、β是两个不同的平面,考查下列命题,其中正确的命题是( )
A.m⊥α,n β,m⊥n
β,m⊥n α⊥β
B.α∥β,m⊥α,n∥β
α⊥β
B.α∥β,m⊥α,n∥β m⊥n
m⊥n
C.α⊥β,m⊥α,n∥β m⊥n
D.α⊥β,α∩β=m,m⊥n
m⊥n
D.α⊥β,α∩β=m,m⊥n n⊥β
n⊥β
6.(理)已知直线m,n和平面α,那么m∥n的一个必要但非充分条件是( )
A.m∥α,n∥α B.m⊥α,n⊥α
C.m∥α且n α D.m,n与α成等角
α D.m,n与α成等角
(文)函数f(x)=log3(x2-2x-8)的唯调减区间为( )
A.(-∞,1) B.(-∞,-2)
C.(4,+∞) D.(-∞,1]
5.(理)设m,n是两条不同的直线,α、β是两个不同的平面,考查下列命题,其中正确的命题是( )
A.m⊥α,n β,m⊥n
β,m⊥n α⊥β
B.α∥β,m⊥α,n∥β
α⊥β
B.α∥β,m⊥α,n∥β m⊥n
m⊥n
C.α⊥β,m⊥α,n∥β m⊥n
D.α⊥β,α∩β=m,m⊥n
m⊥n
D.α⊥β,α∩β=m,m⊥n n⊥β
n⊥β
(文)函数y= (-1≤x<0)的反函数是( )
(-1≤x<0)的反函数是( )
A.y=- (
(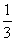 <x≤1)
B.y=-
<x≤1)
B.y=- (x≥
(x≥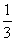 )
)
C.y= (
(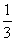 <x≤1)
D.y=
<x≤1)
D.y= (x≥
(x≥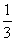 )
)
4.(理)已知函数在f(x)=logsin1(x2-6x+5)在(a,+∞)上是减函数,则实数a的取值范围为( )
A.(5,+∞) B.[5,+∞)
C.(-∞,3) D.(3,+∞)
(文)定义在R上的函数y=f(x)的值域为[a,b],则y=f(x+1)的值域为( )
A.[a,b] B.[a+1,b+1]
C.[a-1,b-1] D.无法确定
3.(理)函数y= (-1≤x<0)的反函数是( )
(-1≤x<0)的反函数是( )
A.y=- (
(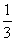 <x≤1)
B.y=-
<x≤1)
B.y=- (x≥
(x≥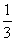 )
)
C.y= (
(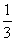 <x≤1)
D.y=
<x≤1)
D.y= (x≥
(x≥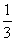 )
)
(文)函数y= 的定义域是( )
的定义域是( )
A.(3,+∞) B.[3,+∞)
C.(4,+∞) D.[4,+∞)
2.(理)函数f(x)= +lg(3x+1)的定义域是( )
+lg(3x+1)的定义域是( )
A.(-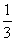 ,+∞)
B.(-
,+∞)
B.(-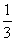 ,1)
,1)
C.(-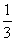 ,
,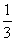 )
D.(-∞,-
)
D.(-∞,-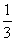 )
)
(文)一个容量为20的样本数据,分组后,组别与频数如下:
|
组别 |
(10,20] |
(20,30] |
(30,40] |
(40,50] |
(50,60] |
(60,70] |
|
频数 |
2 |
3 |
4 |
5 |
4 |
2 |
则样本在(20,50]上的频率为( )
A.12% B.40% C.60% D.70%
1.(理)设f:x→x2是集合A到集合B的映射,如果B={1,2},则A∩B等于( )
A.{1}
B. C.
C. 或{1}
D.
或{1}
D. 或{2}
或{2}
(文)已知集合A={x|x2-5x+6≤0},集合B={x||2x-1|>3},则集合A∩B=( )
A.{x|2<x≤3} B.{x|2≤x<3}
C.{x|2≤x≤3} D.{x|-1<x<3}
20.(本小题满分14分)
设数列{an}是首项为4,公差为1的等差数列,Sn为数列{bn}的前n项和,且
(I)求{an}及{bn}的通项公式an和bn.
(II)若 成立?若存在,求出k的值;若不存在,说明理由;
成立?若存在,求出k的值;若不存在,说明理由;
(III)若对任意的正整数n,不等式 恒成立,求正数a的取值范围.
恒成立,求正数a的取值范围.
19.(本小题满分14分)
双曲线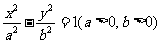 的离心率为2,坐标原点到直线AB的距离为
的离心率为2,坐标原点到直线AB的距离为 ,其中
,其中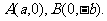
(I)求双曲线的方程;
(II)若B1是双曲线虚轴在y轴正半轴上的端点,点M、N在双曲线上,且 ,求
,求 时,直线MN的方程.
时,直线MN的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com