2．函数的定义域为，设．

(1)求证： ；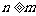

(2)确定t的范围使函数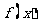在上是单调函数；

(3)求证：对于任意的，总存在，满足；并确定这样的的个数．

1．已知函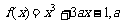数为实常数．

(1)a在什么范围内时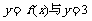，只有一个公共点？

(2)若上有最小值2，求a的值．

26.(本小题14分)

(理)如图，矩形ABCD，|AB|=1，|BC|=a，PA⊥面ABCD且|PA|=1

(1)BC边上是否存在点Q，使得FQ⊥QD，并说明理由；

(2)若BC边上存在唯一的点Q使得FQ⊥QD，指出点Q的位置，并求出此时AD与平面PDQ所成的角的正弦值；

(3)在(2)的条件下，求二面角Q-PD-A的正弦值.

(文)如图，正三棱柱ABC-A₁B₁C₁的底面边长为a，点M在边BC上，△AMC₁是以点M为直角顶点的等腰直角三角形.

(1)求证：点M为边BC的中点；

(2)求点C到平面AMC₁的距离；

(3)求二面角M-AC₁-C的大小.

25.(本小题14分)

(理)某人居住在城镇的A处，准备开车到单位B处上班，若该地各路段发生堵车事件都是相互独立的，且在同一路段发生堵车事件最多只有一次，发生堵车事件的概率如图.(例如：A→C→D算作两个路段：路段AC发生堵车事件的概率为，路段CD发生堵车事件的概率为)

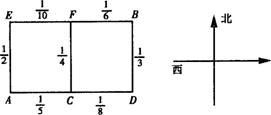
(1)请你为其选择一条由A到B的最短路线(即此人只选择从西向东和从南向北的路线)，使得途中发生堵车事件的概率最小；

(2)若记路线A→C→F→B中遇到堵车次数为随机变量ξ，求ξ的数学期望Eξ.

(文)同时抛掷15枚均匀的硬币一次，

(1)试求至多有1枚正面向上的概率；

(2)试问出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率是否相等?请说明理由.

24.(本小题13分)

(理)设点P(x，y)(x≥0)为平面直角坐标系xOy中的一个动点(其中O为坐标原点)，点P到定点M(，0)的距离比点P到x轴的距离大.

(1)求点P的轨迹方程，并说明它表示什么曲线；

(2)若直线l与点P的轨迹相交于A、B两点，且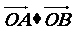=0，点O到直线l的距离为，求直线l的方程.

(文)设点P(x，y)(y≥0)为平面直角坐标系xOy中的一个动点(其中O为坐标原点)，点P到定点M(0，)的距离比点P到x轴的距离大.

(1)求点P的轨迹方程；

(2)若直线l：y=x+1与点P的轨迹相交于A、B两点，求线段AB的长；

(3)设点P的轨迹是曲线C，点Q(1，y₀)是曲线C上一点，求过点Q的曲线C的切线方程.

23.(本小题13分)

(理)已知函数f(x)=2^x-1的反函数为f^-1(x)，g(x)=log₄(3x+1)

(1)用定义证明f^-1(x)在定义域上的单调性；

(2)若f^-1(x)≤g(x)，求x的取值集合D；

(3)设函数H(x)=g(x)-f^-1(x)，当x∈D时，求函数H(x)的值域.

(文)已知函数f(x)=2^x-1的反函数为f^-1(x)，g(x)=log₄(3x+1)

(1)f^-1(x)；

(2)用定义证明f^-1(x)在定义域上的单调性；

(3)若f^-1(x)≤g(x)，求x的取值范围.

22.定义在(-∞，+∞)上的偶函数f(x)满足f(x+1)=-f(x)，且在[-1，0]上是增函数，下面是关于f(x)的判断：

①f(x)是周期函数；

②f(x)的图像关于直线x=1对称；

③f(x)在[0，1]上是增函数；

④f(2)=f(0).

其中正确的判断是_____________________(把你认为正确的判断都填上)

21.已知A箱内有1个红球和5个白球，B箱内有3个白球，现随意从A箱中取出3个球放入B箱，充分搅匀后再从中随意取出3个球放人4箱，共有_________种不同的取法，又红球由A箱移人到B箱，再返回到A箱的概率等于___________.

20.(理)椭圆ax²+by²=1与直线y=-x+1交于A、B两点，过原点与线段AB中点的直线斜率为，则=______________.

(文)已知椭圆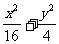=1内一点A(1，1)，则过点A且被该点平分的弦所在直线的方程是_________________________.

19.如图，将正方形按ABCD沿对角线AC折成二面角D-AC-B，使点B、D的距离等于AB的长.此时直线AB与CD所成的角的大小为____________________.