7．已知等差数列的前n项和为S_n，且S₂₀₀ = 100，A、B、C为平面内三点，点O为平面外任意一点，若，则A、B、C　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．共线　　　　　　　　　　　　　　　　　　　　　　　　　 B．不共线

　　　 C．共线与否和点O的位置有关　　　　　　　 D．位置关系不能确定

6．若等差数列和等比数列的首项均为1，且公差d>0，公比q > 1，则集合　 　的元素个数最多有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．1　　　　　　　　　　　　 B．2　　　　　　　　　　　　 C．3　　　　　　　　　　　　 D．4

5．算法

　 S₁：输入n，

　 S₂：判断n是否是2

　 若n = 2，则n满足条件

　 若n > 2，则执行S₃

　 S₃：依次从2到n－1检验能不能整除n，若不能整除n满足条件，上述满足条件的数是　　　　　　　　　　　　　　　 (　　 )

　　　 A．质数　　　　　　　　　 B．奇数　　　　　　　　　 C．偶数　　　　　　　　　 D．4的倍数

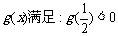4．若的反函数，则函数的图像向左平移一个单位后的图像大致是下图中的　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

3．若关于x的不等式的解集是M，则对任意实数k，总有　　　　 (　　 )

　　　 A．2∈M，0M　　　 B．2M，0M　　　 C．2∈M ，0∈M　　 D．2M，0∈M

2．对于线性相关系数r，以下说法正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．r只能为正值，不能为负值

　　　 B．|r|≤1，且|r|越接近于1，相关程度越大；相反则越小

　　　 C．|r|≤1，且|r|越接近于1，相关程度越小；相反则越大

　　　 D．以上均不对

1．复数，则实数a的取值范围是　　　　　　　 (　　 )

　　　 A．　　　　　　　　　　　　　　　　　　　　 B．　　　　　　　　

　　　 C．　　　　　　　　　　　　　　　　　　　　　　　　 D．

22．(本小题满分12分)

某化工企业生产某种化工原料，在生产过程中对周边环境将造成一定程度的污染，过去没有采取任何治理污染的措施，依据生产和营销的统计数据发现，该企业每季度的最大生产能力为2万吨，且每生产x万吨化工原料，获得的纯利润y(百万元)近似地满足：y=(x+1)ln(x+1).自2007年3月人民代表大会召开后，该企业认识到保护环境的重要性，决定投入资金进行的污染治理，计划用于治理污染的资金总费用为y₁=2px(百万元)(其中x为该工厂的生产量，p为环保指标参数，p∈.

　 (I)试写出该企业进行污染治理后的利润函数；

　 (II)试问p控制在什么范围内，该企业开始进行污染治理的第一个季度，在最大生产能力的范围内始终不会出现亏损？

21．(本小题满分12分)

已知，直线l：y=－2，动点P到直线l的距离为d，且d=.

　 (I)求动点P的轨迹方程；

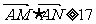　 (II)直线m:y=与点P的轨迹交于M、N两点，当时，求直线m的倾斜角α的取值范围；

　 (III)设直线h与点P的轨迹交于C、D两点，写出命题“如果直线h过点B，那么=－12”的逆命题，并判断该逆命题的真假，请说明理由.

20．(本小题满分12分)

在一个盒子里放有6张卡片，上面标有数字1，2，3，4，5，6，现在从盒子里每次任意取出一张卡片，取两片.

　 (I)若每次取出后不再放回，求取到的两张卡片上数字之积大于12的概率；

　 (II)在每次取出后再放回和每次取出后不再放回这两种取法中，得到的两张卡片上的最大数字的期望值是否相等？请说明理由.