
3.“ ”是“
”是“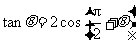 ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
2.设变量 满足约束条件
满足约束条件 则目标函数
则目标函数 的最大值为( )
的最大值为( )
A.4 B.11 C.12 D.14
1. 是虚数单位,
是虚数单位, ( )
( )
A. B.
B.  C.
C. D.
D.
(17)(本小题满分12分)
在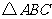 中,已知
中,已知 ,
, ,
, .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的值.
的值.
(18)(本小题满分12分)
已知甲盒内有大小相同的3个红球和4个黑球,乙盒内有大小相同的5个红球和4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为红球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
(19)(本小题满分12分)
如图,在四棱锥 中,
中, 底面
底面 ,
,
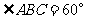 ,
, ,
, 是
是 的中点.
的中点.
 (Ⅰ)求
(Ⅰ)求 和平面
和平面 所成的角的大小;
所成的角的大小;
(Ⅱ)证明 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.
(20)(本小题满分12分)
在数列 中,
中, ,
, ,
, .
.
(Ⅰ)证明数列 是等比数列;
是等比数列;
(Ⅱ)求数列 的前
的前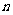 项和
项和 ;
;
(Ⅲ)证明不等式 ,对任意
,对任意 皆成立.
皆成立.
(21)(本小题满分14分)
设函数 (
(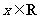 ),其中
),其中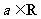 .
.
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点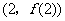 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求函数
时,求函数 的极大值和极小值;
的极大值和极小值;
(Ⅲ)当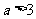 时,证明存在
时,证明存在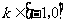 ,使得不等式
,使得不等式 对任意的
对任意的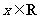 恒成立.
恒成立.
(22)(本小题满分14分)
设椭圆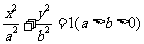 的左、右焦点分别为
的左、右焦点分别为 是椭圆上的一点,
是椭圆上的一点, ,原点
,原点 到直线
到直线 的距离为
的距离为 .
.
(Ⅰ)证明 ;
;
(Ⅱ)求 使得下述命题成立:设圆
使得下述命题成立:设圆 上任意点
上任意点 处的切线交椭圆于
处的切线交椭圆于 ,
, 两点,则
两点,则 .
.
(11)从一堆苹果中任取了20只,并得到它们的质量(单位:克)数据分布表如下:
|
分组 |
 |
 |
 |
 |
 |
 |
|
频数 |
1 |
2 |
3 |
10 |
|
1 |
则这堆苹果中,质量不小于120克的苹果数约占苹果总数的 %.
(12) 的二项展开式中常数项是
(用数字作答).
的二项展开式中常数项是
(用数字作答).
(13)一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为 ,
, ,
,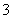 ,则此球的表面积为 .
,则此球的表面积为 .
(14)已知两圆 和
和 相交于
相交于 两点,则直线
两点,则直线 的方程是 .
的方程是 .
(15)在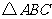 中,
中, ,
, ,
, 是边
是边 的中点,则
的中点,则 .
.
 (16)如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同,且两端的格子的颜色也不同,则不同的涂色方法共有 种(用数字作答).
(16)如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同,且两端的格子的颜色也不同,则不同的涂色方法共有 种(用数字作答).
(1)已知集合 ,
, ,则
,则 ( )
( )
A. B.
B.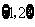 C.
C. D.
D.
(2)设变量 满足约束条件
满足约束条件 则目标函数
则目标函数 的最大值为( )
的最大值为( )
A.10 B.12 C.13 D.14
(3) “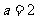 ”是“直线
”是“直线 平行于直线
平行于直线 ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
(4)设 ,
, ,
, ,则( )
,则( )
A.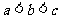 B.
B. C.
C.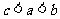 D.
D.
(5)函数 的反函数是( )
的反函数是( )
A. B.
B.
C. D.
D.
(6)设 为两条直线,
为两条直线,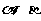 为两个平面,下列四个命题中,正确的命题是( )
为两个平面,下列四个命题中,正确的命题是( )
A.若 与
与 所成的角相等,则
所成的角相等,则
B.若 ,
, ,
, ,则
,则
C.若 ,
,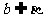 ,
, ,则
,则
D.若 ,
, ,
, ,则
,则
(7)设双曲线 的离心率为
的离心率为 ,且它的一条准线与抛物线
,且它的一条准线与抛物线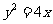 的准线重合,则此双曲线的方程为( )
的准线重合,则此双曲线的方程为( )
A.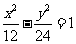 B.
B.
C. D.
D.
(8)设等差数列 的公差
的公差 不为0,
不为0, .若
.若 是
是 与
与 的等比中项,则
的等比中项,则 ( )
( )
A.2 B.4 C.6 D.8
(9)设函数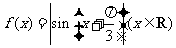 ,则
,则 ( )
( )
A.在区间 上是增函数 B.在区间
上是增函数 B.在区间 上是减函数
上是减函数
C.在区间 上是增函数 D.在区间
上是增函数 D.在区间 上是减函数
上是减函数
(10)设 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当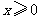 时,
时, ,若对任意的
,若对任意的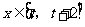 ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.
D.
第Ⅱ卷
本卷共12小题,共100分.
(17)(本小题满分12分)
设数列 满足a1+3a1+32a1+…+3n-1an=
满足a1+3a1+32a1+…+3n-1an= .
.
(Ⅰ)求数列 的通项;
的通项;
(Ⅱ)设bn= ,求数列
,求数列 的前n项和Sn.
的前n项和Sn.
(18)(本小题满分12分)
设b和c分别是先后抛掷一枚骰子得到的点数,用随机变量 表示方程
表示方程 实根的个数(重根按一个计)
实根的个数(重根按一个计)
(Ⅰ)求方程 有实根的概率;
有实根的概率;
(Ⅱ)求 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)求在先后两次出现的点数中有5的条件下,方程 有实根的概率。
有实根的概率。
(19)(本小题满分12分)
如图,在直四棱柱ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB//DC
(Ⅰ)设E是DC的中点,求证:D1E//平面A1BD;
(Ⅱ)求二面角A1-BD-C1的余弦值。

(20)(本小题满分12分)
 如图,甲船以每小时30
如图,甲船以每小时30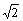 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A1处时,乙船航行到甲船的北偏西120°方向的B1处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A1处时,乙船航行到甲船的北偏西120°方向的B1处,此时两船相距10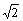 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
(21)(本小题满分12分)
已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3;最小值为1;
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线l过定点,并求出该定点的坐标.
(22)(本小题满分14分)
设函数f(x)=x2+b ln(x+1),其中b≠0.
(Ⅰ)当b> 时,判断函数f(x)在定义域上的单调性;
时,判断函数f(x)在定义域上的单调性;
(Ⅱ)求函数f(x)的极值点;
(Ⅲ)证明对任意的正整数n,不等式ln )都成立.
)都成立.
(13)设O是坐标原点,F是抛物线y2=2px(p>0)的焦点,A是抛物线上的一点,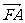 与x轴正向的夹角为60°,则
与x轴正向的夹角为60°,则 为
.
为
.
(14)设D是不等式组 表示的平面区域,则D中的点P(x,y)到直线x+y=10距离的最大值是
.
表示的平面区域,则D中的点P(x,y)到直线x+y=10距离的最大值是
.
(15)与直线x+y-2=0和曲线x2+y2-12x-12y+54=0都相切的半径最小的圆的标准方程是 .
(16)函数y=loga(x+3)-1(a>0,a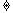 1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中mn>0,则
1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中mn>0,则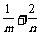 的最小值为
.
的最小值为
.
12.位于坐标原点的一个质点 按下述规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上、向右移动的概率者是
按下述规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上、向右移动的概率者是 ,质点
,质点 移动五次后位于点(2,3)的概率是
移动五次后位于点(2,3)的概率是
(A)  (B)
(B)  (C)
(C)
 (D)
(D)

11.在直角△ABC中,CD是斜边AB上的高,则下列等式不成立的是
(A) (B)
(B)

(C)  (D)
(D) 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com