
20.(本小题满分12分)
已知双曲线 的左、右焦点分别为
的左、右焦点分别为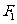 ,
, ,过点
,过点 的动直线与双曲线相交于
的动直线与双曲线相交于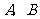 两点.
两点.
(I)若动点 满足
满足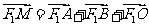 (其中
(其中 为坐标原点),求点
为坐标原点),求点 的轨迹方程;
的轨迹方程;
(II)在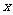 轴上是否存在定点
轴上是否存在定点 ,使
,使 ·
·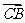 为常数?若存在,求出点
为常数?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
19.(本小题满分12分)
如图4,某地为了开发旅游资源,欲修建一条连接风景点 和居民区
和居民区 的公路,点
的公路,点 所在的山坡面与山脚所在水平面
所在的山坡面与山脚所在水平面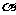 所成的二面角为
所成的二面角为 (
( ),且
),且 ,点
,点 到平面
到平面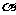 的距离
的距离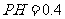 (km).沿山脚原有一段笔直的公路
(km).沿山脚原有一段笔直的公路 可供利用.从点
可供利用.从点 到山脚修路的造价为
到山脚修路的造价为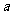 万元/km,原有公路改建费用为
万元/km,原有公路改建费用为 万元/km.当山坡上公路长度为
万元/km.当山坡上公路长度为 km(
km( )时,其造价为
)时,其造价为 万元.已知
万元.已知 ,
, ,
, ,
, .
.
(I)在 上求一点
上求一点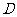 ,使沿折线
,使沿折线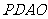 修建公路的总造价最小;
修建公路的总造价最小;
(II) 对于(I)中得到的点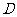 ,在
,在 上求一点
上求一点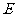 ,使沿折线
,使沿折线 修建公路的总造价最小.
修建公路的总造价最小.
(III)在 上是否存在两个不同的点
上是否存在两个不同的点 ,
, ,使沿折线
,使沿折线 修建公路的总造价小于(II)中得到的最小总造价,证明你的结论.
修建公路的总造价小于(II)中得到的最小总造价,证明你的结论.


18.(本小题满分12分)
如图2,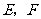 分别是矩形
分别是矩形 的边
的边 的中点,
的中点, 是
是 上的一点,将
上的一点,将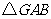 ,
, 分别沿
分别沿 翻折成
翻折成 ,
,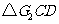 ,并连结
,并连结 ,使得平面
,使得平面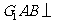 平面
平面 ,
, ,且
,且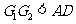 .连结
.连结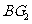 ,如图3.
,如图3.




图2 图3
(I)证明:平面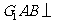 平面
平面 ;
;
(II)当 ,
,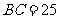 ,
, 时,求直线
时,求直线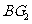 和平面
和平面 所成的角.
所成的角.
17.(本小题满分12分)
某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力,每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有60%,参加过计算机培训的有75%,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(I)任选1名下岗人员,求该人参加过培训的概率;
(II)任选3名下岗人员,记 为3人中参加过培训的人数,求
为3人中参加过培训的人数,求 的分布列和期望.
的分布列和期望.
16.(本小题满分12分)
已知函数 ,
, .
.
(I)设 是函数
是函数 图象的一条对称轴,求
图象的一条对称轴,求 的值.
的值.
(II)求函数 的单调递增区间.
的单调递增区间.
15.将杨辉三角中的奇数换成1,偶数换成0,得到如图1所示的0-1三角数表.从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第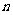 次全行的数都为1的是第 行;第61行中1的个数是 .
次全行的数都为1的是第 行;第61行中1的个数是 .
第1行 1 1
第2行 1 0 1
第3行 1 1 1 1
第4行 1 0 0 0 1
第5行 1 1 0 0 1 1
…… ………………………………………
图1
14.设集合 ,
,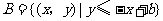 ,
, ,
,
(1) 的取值范围是 ;
的取值范围是 ;
(2)若 ,且
,且 的最大值为9,则
的最大值为9,则 的值是
.
的值是
.
13.函数 在区间
在区间 上的最小值是 .
上的最小值是 .
12.在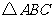 中,角
中,角 所对的边分别为
所对的边分别为 ,若
,若 ,b=
,b= ,
,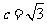 ,
, ,则
,则 .
.
11.圆心为 且与直线
且与直线 相切的圆的方程是 .
相切的圆的方程是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com