22．请考生在A、B两题中选一题作答，如果多做，则按所做的第一题记分。作答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑。

A：(本小题满分10分)选修4－1：几何证明选讲

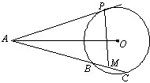
如图，已知AP是⊙O的切线，P为切点，AC是⊙O的割线，与⊙O交于B，C两点，圆心O在∠PAC的内部，点M是BC的中点。

(Ⅰ)证明 A，P，O，M四点共圆；

(Ⅱ)求∠OAM+∠APM的大小。

B：(本小题满分10分)选修4－4：

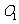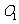坐标系与参数方程⊙和⊙的极坐标方程分别为。

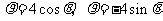(Ⅰ)把⊙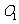和⊙的极坐标方程化为直角坐标方程；

(Ⅱ)求经过⊙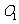，⊙交点的直线的直角坐标方程。

21．(本小题满分12分)

在平面直角坐标系xOy中，已知圆的圆心为Q，过点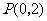且斜率为k的直线与圆Q相交于不同的两点A，B。

(Ⅰ)求k的取值范围；

(Ⅱ)是否存在常数k，使得向量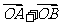与共线？如果存在，求k值；如果不存在，请说明理由。

20．(本小题满分12分)

设有关于x的一元二次方程。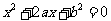

(Ⅰ)若a是从0，1，2，3四个数中任取的一个数，b是从0，1，2三个数中任取的一个数，求上述方程有实根的概率。

(Ⅱ)若a是从区间［0，3］任取的一个数，b是从区间［0，2］任取的一个数，求上述方程有实根的概率。

19．(本小题满分12分)

设函数

(Ⅰ)讨论的单调性；

(Ⅱ)求在区间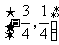的最大值和最小值。

18．(本小题满分12分)

如图，A，B，C，D为空间四点．在△ABC中，AB=2，。等边三角形ADB以AB为轴运动。

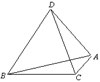
(Ⅰ)当平面ADB⊥平面ABC时，求CD；

(Ⅱ)当△ABD转动时，是否总有AB⊥CD？证明你的结论。

17．(本小题满分12分)

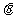如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个侧点C与D。现测得，并在点C测得塔顶A的仰角为，求塔高AB。

16．已知是等差数列，，其前5项和，则其公差d=　　。

15．是虚数单位， 　　　。(用的形式表示，)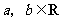

14．设函数f(x)=(x+1)(x+a)为偶函数，则a=　　。

13．已知双曲线的顶点到渐近线的距离为2，焦点到渐近线的距离为6，则该双曲线的离心率为 　　　。