
22.(本小题满分14分)
已知函数 在
在 与
与 时都取得极值。
时都取得极值。
(1)求 的值及函数
的值及函数 的单调区间;
的单调区间;
(2)当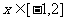 时,
时, 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(3)证明:对 内的任意两个值
内的任意两个值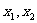 ,都有
,都有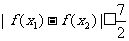
21.(本小题满分12分)
在一次考试后,对某一班级的前六名学生的数学分数 ,物理分数
,物理分数 ,语文分数
,语文分数 及相关数据进行了统计.如表:
及相关数据进行了统计.如表:
|
学生 |
 |
 |
 |
 |
 |
 |
 |
 |
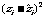 |
|
1 |
125 |
94 |
107 |
56.25 |
20.25 |
2.25 |
33.75 |
0.9 |
0 |
|
2 |
124 |
96 |
102 |
42.25 |
42.25 |
12.25 |
42.25 |
3.2 |
23 |
|
3 |
114 |
88 |
112 |
12.25 |
2.25 |
42.25 |
5.25 |
1.1 |
54 |
|
4 |
120 |
90 |
111 |
6.25 |
0.25 |
30.25 |
1.25 |
1.7 |
26 |
|
5 |
111 |
85 |
103 |
42.25 |
20.25 |
6.25 |
29.25 |
0.2 |
1 |
|
6 |
111 |
84 |
98 |
42.25 |
30.25 |
56.25 |
35.75 |
0.6 |
36 |
|
和 |
705 |
537 |
633 |
200 |
115.5 |
150 |
146 |
7.7 |
140 |
注:表中部分数字是近似值.
(1)用变量 与
与 的相关系数说明物理与数学的相关程度;(取
的相关系数说明物理与数学的相关程度;(取 )
)
(2)求 与
与 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(3)若一学生的数学分数是100,你预报他的物理分数是多少?
(4)用相关指数比较物理与数学,语文与数学的回归模型效果.
20.(本小题满分12分)
已知函数 .
.
(1)若 无极值,求
无极值,求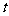 的取值范围;
的取值范围;
(2)确定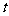 的值,使
的值,使 的极小值为0
的极小值为0
19.甲,乙二人进行乒乓球比赛,甲每局获胜的概率均为 .现在他们进行一场“五局三胜制”的比赛,即先胜三局者胜,比赛停止.若甲先胜了第一局.
.现在他们进行一场“五局三胜制”的比赛,即先胜三局者胜,比赛停止.若甲先胜了第一局.
(1)求乙取胜的概率;
(2)比赛打满五局的概率;
(3)设比赛局数为 ,求
,求 的分布列及
的分布列及 .
.
19.(本小题满分12分)
18.(本小题满分12分)
已知二项式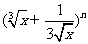 的展开式中奇数项的二项式系数之和是128.
的展开式中奇数项的二项式系数之和是128.
(1)求n;
(2)展开式中有理项共有多少项?
(3)求展开式中系数最大的项.
17. (本小题满分12分)
已知z是复数, 和
和 均为实数.
均为实数.
(1)求复数z;
(2)若复数 对应点在复平面内的第三象限,求实数t的取值范围.
对应点在复平面内的第三象限,求实数t的取值范围.
16.下列命题:
①用相关指数R2来刻画回归的效果时,R2的值越大,说明模型拟合的效果越好;
②对分类变量X与Y的随机变量K2的观测值k来说,k越小,“X与Y有关系”可信程度越大;
③两个随机变量相关性越强,则相关系数的绝对值越接近1;
④三维柱形图中柱的高度表示的是各分类变量的频数;
其中正确命题的序号是 .(写出所有正确命题的序号)
15. 从集合{O,P,Q,R,S}与{0,1,2,3,4,5,6}中各任选2个元素排成一排(字母和数字均不能重复).每排中字母O,Q和数字0至多只能出现一个的不同排法种数是________.(用数字作答).
14. 函数 在区间
在区间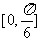 上的最大值是
。
上的最大值是
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com