
8.连掷两颗骰子,则两次掷得的骰子向上的点数之和不大于4的概率是
(A) (B)
(B) (C)
(C) (D)
(D)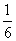
7.设a、b、c是平面内的非零向量,则下列命题中正确的是
(A)若 ,则
,则
(B)
(C)若 ,则
,则
(D)若 ,则
,则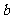 ∥
∥
6.给出四个数:① ;②
;②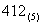 ;③
;③ ;④
;④ 。其中相等的两个数是
。其中相等的两个数是
(A)①② (B)①③ (C)②③ (D)②④
5.如下图所示,程序运行后输出的结果为

(A)22;-22 (B)-22;22 (C)-5;5 (D)5;-5
4.同时掷3枚硬币,下面两个事件中是对立事件的是
(A)至少有1枚正面向上和至多有1枚正面向上
(B)至多有1枚正面向上和至少有2枚正面向上
(C)至多有1枚正面向上和恰好有2枚正面向上
(D)至少有2枚正面向上和恰好有1枚正面向上
3.函数 的单调递增区间是
的单调递增区间是
(A)[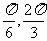 ] (B)[
] (B)[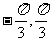 ]
]
(C)[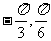 ] (D)[
] (D)[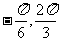 ]
]
2.某同学家开了一个小卖部,为了研究气温对热饮销售的影响,经过统计卖出的热饮杯数与当天气温的对比数据,并结合画出的散点图,求得回归方程为: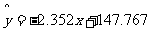 。如果某天的气温是2℃,预测该天卖出的热饮杯数为
。如果某天的气温是2℃,预测该天卖出的热饮杯数为
(A)132 (B)140 (C)143 (D)150+
1.与-2007°角的终边相同的角的集合是
(A) (B)
(B)
(C) (D)
(D)
(17)(本小题满分l2分)
已知函数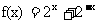
(Ⅰ)判断函数f(x)的奇偶性;
(Ⅱ)证明函数f(x)在(0,+∞)上是增函数。
(18)(本小题满分l2分)
求圆心在直线 上,与x轴相切,且被直线
上,与x轴相切,且被直线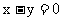 截得的弦长为
截得的弦长为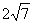 的圆的方程。
的圆的方程。
(19)(本小题满分12分)
已知-l≤x≤0,求函数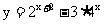 的最大值和最小值。
的最大值和最小值。
(20)(本小题满分l2分)
已知直线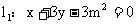 和直线
和直线 相交于点P。
相交于点P。
(Ⅰ)用m表示直线l1与l2的交点P的坐标;
(Ⅱ)当m为何值时,点P到直线 的距离最短;并求出最短距离。
的距离最短;并求出最短距离。
(21)(本小题满分12分)
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=AB,E、F、M分别是线段PD、PC、AB的中点。
(Ⅰ)求证:MF⊥PC;
(Ⅱ)求二面角E-AB-D的平面角。

(22)(本小题满分14分)
已知函数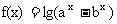 ,其中a>1>b>0。
,其中a>1>b>0。
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)利用函数的单调性判断,在函数f(x)的图像上是否存在不同的两点,使过这两点的直线平行于x轴?并证明你的结论。
(Ⅲ)当a、b满足什么条件时,y=f(x)在区间(1,+∞)上恒取正值?
(13)已知 ,则
,则 。
。
(14)经过点A(3,1),且被圆 所截得的弦长最短的直线方程为
。
所截得的弦长最短的直线方程为
。
(15)已知正方体ABCD-A′B′C′D′中,AB的中点为M,DD′的中点为N,则异面直线B′M与CN所成的角是 。
(16)若函数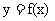 对于任意的x,y
对于任意的x,y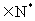 ,都有
,都有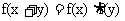 ,且f(1)=2,则
,且f(1)=2,则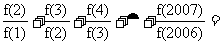 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com