
5.已知某单位有女职工120人,男职工有90人,现采用分层抽样(按男、女分层)抽取一个样本,若已知样本中有27名男职工,则样本容量为
A.、60 B、 68 C、54 D、63
4、在120个零件中,一级品24个,二级品36个,三级品60个,用系统抽样法从中抽取容量为20的样本,则每个个体被抽到的概率是
A、 B、 C、 D、
3、右边是计算一个函数值的算法框图,那么这个函数的解析式是
A、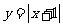 B、
B、
C、 D、
D、
2.算法:
第一步:输入正整数n
第二步:判断n是否等于2,若n=2,则输出n,结束;若n>2,则执行第四步
第三步:执行第五步
第四步:依次从2到n-1检验能不能整除n,若不能整除n,则输出n,结束;否则执行第五步
 第五步:输出“不满足条件”,结束。
第五步:输出“不满足条件”,结束。
这个算法如果输出n的值,那么这个n是
A.质数 B.奇数
C.偶数 D.一定是2
1.某社区有500户家庭,其中高收入家庭125户,中等收入家庭280户,低收入家庭95户,为了调查社会购买力的某项指标,要从中抽取1个容量为100户的样本,记作抽样①;
某学校高三年级有12名足球运动员,要从中选出3人调查学习负担情况,记作抽样②。
那么完成上述两项调查应采用的适当的抽样方法是
A、①用简单随机抽样法,②用系统抽样法
B、①用分层抽样法,②用简单随机抽样法
C、①用系统抽样法,②用简单随机抽样法
D、①用分层抽样法,②用系统抽样法
22、已知函数f(x)的定义域为[0,1],且满足下列条件:
①对于任意x∈[0,1],总有f(x)≥3,且f(1)=4;
②若x1≥0,x2≥0,x1+x2≤1,则有f(x1+x2)≥f(x1)+f(x2)-3.
(Ⅰ)求f(0)的值;
(Ⅱ)求证:f(x)≤4;
(Ⅲ)证明:f(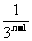 )≤
)≤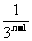 +3(n∈N*);
+3(n∈N*);
(Ⅳ)当x∈(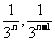 ](n=1,2,3,……)时,试证明f(x)<3x+3.
](n=1,2,3,……)时,试证明f(x)<3x+3.
21、在数列 中,
中, ,
,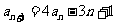 ,
,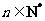 .
.
(Ⅰ)证明:数列 是等比数列;
是等比数列;
(Ⅱ)求数列 的前
的前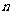 项和
项和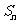 ;
;
(Ⅲ)若 对任意
对任意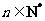 皆成立,求实数λ的最小值.
皆成立,求实数λ的最小值.
20、如图,有一块半椭圆形钢板,其长半轴长为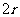 ,短半轴长为
,短半轴长为 .计划将此钢板切割成等腰梯形的形状,下底
.计划将此钢板切割成等腰梯形的形状,下底 是半椭圆的短轴,上底
是半椭圆的短轴,上底 的端点在椭圆上,记
的端点在椭圆上,记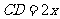 ,梯形面积为
,梯形面积为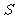 .
.
 (Ⅰ)求面积
(Ⅰ)求面积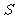 以
以 为自变量的函数式,并写出其定义域;
为自变量的函数式,并写出其定义域;
(Ⅱ)求面积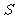 的最大值.
的最大值.
19、如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(Ⅰ)求点B到平面A1C1CA的距离;
(Ⅱ)求二面角B-A1D-A的大小;
(Ⅲ)在线段AC上是否存在一点F,使得EF⊥平面A1BD?若存在,确定其位置并证明结论;若不存在,说明理由.

18、若函数f(x)= sin2ωx-sinωxcosωx(ω>0)的图象与直线y=m (m为常数)相切,并且切点的横坐标依次成公差为 的等差数列.
的等差数列.
(Ⅰ)求m的值;
(Ⅱ)若点A(x0,y0)是y=f(x)图象的对称中心,且x0∈[0, ],求点A的坐标.
],求点A的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com