22．(本小题满分14分)

对所表示的平面区域为D_n，把D_n内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列：，

.

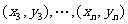　 (Ⅰ)求；

　 (Ⅱ)数列{a_n}满足a₁=x₁，且时，　　　　 ；

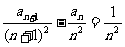　 (Ⅲ)在(Ⅱ)的条件下，试比较(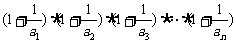与4的大小关系.

21．(本小题满分12分)

已知函数的图象在x=2处的切线互相平行.

　 (Ⅰ)求t的值；

　 (Ⅱ)设恒成立，求a的取值范围.

20．(本小题满分12分)

　　　 新星家具厂开发了两种新型拳头产品，一种是模拟太空椅，一种是多功能办公桌. 2005年该厂生产的模拟太空椅获利48万元，以后它又以上年利润的1.25倍的速度递增；而多功能办公桌在同年获利75万元，这个利润是上年利润的，以后每年的利润均以此方式产生，预期计划若干后两产品利润之和达到174万元，从2005年起：

　 (1)哪一年两产品获利之和最小？

　 (2)至少经过几年即可达到或超过预期计划？

19．(本小题满分12分)

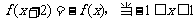　　　 设上的奇函数，对任意实数x，都有时，

　 (Ⅰ)求证：直线x=1是函数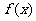图象的一条对称轴；

　 (Ⅱ)当时，求函数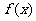的解析式.

18．(本小题满分12分)

在△ABC中，设内角A、B、C的对边分别为a、b、c，向量m=(cosA, sinA)，

n=，若|m+n|=2.

　 (Ⅰ)求角A的大小；

　 (Ⅱ)若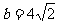，且c=a，求△ABC的面积.

17．(本小题满分12分)

已知等差数列{a_n}的前n项和为S_n，且a₃=5，S₁₅=225.

　 (Ⅰ)求数列{a_­n}的通项a_n；

　 (Ⅱ)设b_n=+2n，求数列{b_n}的前n项和T_n.

16．考察下列一组不等式：

　　 2³+5³>2²·5+2·5²，

　　 2⁴+5⁴>2³·5+2·5³，

　　 2+5>2²·5+2·5²，

………………

将上述不等式在左右两端仍为两项和的情况下加以推广，使以上的不等式成为推广不等式的特例，则推广的不等式为　　　　　　　　　　　　　 .

15．函数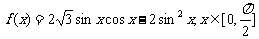的最小值为　　　　

14．一船向正北匀速行驶，看见正西方两座相距10浬的灯塔恰好与该船在同一直线上，继续航行半小时后，看见其中一座灯塔在南偏西60°方向上，另一灯塔在南偏西75°方向上，则该船的速度是　　 　　　浬/小时.

13．函数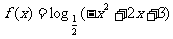的单调递增区间为