
20.(本小题满分16分)
已知: ,数列
,数列 的前n项和为
的前n项和为 ,点
,点 在曲线
在曲线
(1)求数列 的通项公式;
的通项公式;
(2)数列 的前n项和为Tn,且满足
的前n项和为Tn,且满足 ,设定
,设定 的值,使得数列
的值,使得数列 是等差数列;
是等差数列;
(3)求证: .
.
19.(本题满分16分)
设函数 ,已知
,已知 ,且
,且 (a∈R,且a≠0),函数
(a∈R,且a≠0),函数 (b∈R,c为正整数)有两个不同的极值点,且该函数图象上取得极值的两点A、B与坐标原点O在同一直线上。
(b∈R,c为正整数)有两个不同的极值点,且该函数图象上取得极值的两点A、B与坐标原点O在同一直线上。
(1)试求a、b的值;
(2)若 时,函数
时,函数 的图象恒在函数
的图象恒在函数 图象的下方,求正整数
图象的下方,求正整数 的值。
的值。
18.(本小题满分16分)已知点 ,
, ,
, ,
,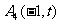 ,
, ,其中
,其中 ,
,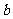 为正常数.
为正常数.

(1)半径为2的圆C1经过 (
(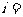 1,2,…,5)这五个点,求b和t的值;
1,2,…,5)这五个点,求b和t的值;
(2)椭圆C2以 ,
, (
( )为焦点,长轴长是4.若
)为焦点,长轴长是4.若 (
(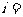 1,2,…,5),试用
1,2,…,5),试用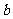 表示
表示 ;
;
(3)在(2)中的椭圆C2中,两线段长的差 ,
, ,…,
,…, 构成一个数列
构成一个数列 ,问
,问 能否对
能否对 1,2,3,4都有
1,2,3,4都有 ?如果能,请给出证明;如果不能,请举出反例.
?如果能,请给出证明;如果不能,请举出反例.
17.(本小题满分14分)
北京奥运会纪念章某特许专营店销售纪念章,每枚进价为5元,同时每销售一枚这种纪念章还需向北京奥组委交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚,经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为 元.
元.
(1)写出该特许专营店一年内销售这种纪念章所获得的利润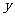 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格 的函数关系式(并写出这个函数的定义域)
的函数关系式(并写出这个函数的定义域)
(2)当每枚纪念销售价格 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润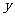 (元)最大,并求出这个最大值.
(元)最大,并求出这个最大值.
16.(本小题满分14分)如图,在四棱锥 中,侧面
中,侧面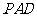 是正三角形,且与底面
是正三角形,且与底面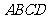 垂直,底面
垂直,底面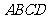 是边长为
是边长为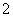 的菱形,
的菱形,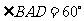 ,
, 是
是 中点,截面
中点,截面 交
交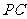 于
于 .
.

(Ⅰ)求证: ;
;
(Ⅱ)求证: ⊥平面
⊥平面 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
15.(本小题满分14分)在 中,三内角A、B、C的对边分别为a、b、c,若
中,三内角A、B、C的对边分别为a、b、c,若 ,
, ,且
,且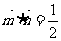 ,(1)求A; (2)若
,(1)求A; (2)若 ,
, 的面积
的面积 ,求
,求 的值。
的值。
14.定义一种运算“*”,它对于正整数n满足以下性质:
(1)2*2007=1 (2)(2n + 2)*2007=3·[(2n)*2007],则2008*2007的值是 .
13.若直线 与圆
与圆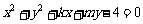 交于M、N两点,并且M、N关于直线
交于M、N两点,并且M、N关于直线 对称,则不等式组
对称,则不等式组 表示的平面区域的面积是
.
表示的平面区域的面积是
.
12.给出下面类比推理命题(其中Q为有理数集,R为实数集,C为复数集):
①“若 ”类比推出“
”类比推出“ ”
”
②“若 ”类比推出
”类比推出
“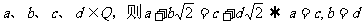 ”
”
③“若 ”类比推出“若
”类比推出“若 ” ④“若
” ④“若 ”类比推出“若
”类比推出“若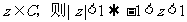 ”
”
其中类比结论正确的命题是 .
11.已知函数 有极大值和极小值,则a的取值范围是 .
有极大值和极小值,则a的取值范围是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com