
3.将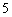 个颜色互不相同的球全部放入编号为
个颜色互不相同的球全部放入编号为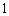 和
和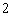 的两个盒子里,使得放入每个盒子里的球个数不小该盒子的编号,则不同的放球方法有( ).
的两个盒子里,使得放入每个盒子里的球个数不小该盒子的编号,则不同的放球方法有( ).
A.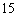 种
B.
种
B.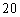 种 C.
种 C. 种 D.
种 D.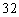 种
种
2.设二项式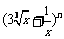 的展开式的各项系数的和为
的展开式的各项系数的和为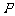 ,所有二项式系数的和为
,所有二项式系数的和为 .若有
.若有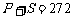 ,则
,则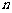 等于( ).
等于( ).
A.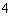 B.
B.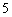 C.
C. D.
D.
1.设集合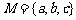 ,
,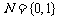 ,映射
,映射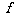 :
: 满足
满足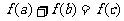 ,则映射
,则映射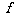 :
: 的个数为( ).
的个数为( ).
A.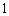 B.
B.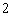 C.
C.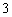 D.
D.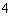
19.某单位有三辆汽车参加某种事故保险,单位年初向保险公司缴纳每辆900元的保险金,对在一年内发生所捉事故的每辆汽车,单位可获9000元的赔偿(假设每辆车最多只赔偿一次)设三辆车在一年内发生所种事故的概率分别为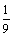 、
、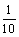 、
、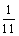 ,且各车是否发生事故相互独立,求一年内该单位在所保险中。
,且各车是否发生事故相互独立,求一年内该单位在所保险中。
(1)获赔的概率 。
(2)获赔金额 的分布列与期望。
的分布列与期望。
18.口袋里装有大小相同的卡片八张,其中三张标有数字1,三张标有数字2,二张标有数字3,第一次从口袋里任里任意抽取一张,放回口袋里后第二次再任意抽取一张,记第一次与第二次取到卡片上数字之和为 .
.
(1) 为何值时,其发生的概率最大?说明理由;
为何值时,其发生的概率最大?说明理由;
(2)求随机变量 的期望
的期望 .
.
17.袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为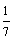 ,现有甲.乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用
,现有甲.乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用 表示取球终止时所需要的取球次数。
表示取球终止时所需要的取球次数。
(I)求袋中原有白球的个数;
(Ⅱ)甲取到白球的概率。
(III)求随机变量 的概率分布列及期望。
的概率分布列及期望。
16.在袋里装有30个小球,其中彩球有: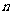 个红色.5个蓝色.10个黄色.其余为白色。求:(1)如果已经从中取定了5个黄球和3个篮球,并将他们编上不同的号码后排成一排,那么使蓝色小球互不相邻的排法有多少种?
个红色.5个蓝色.10个黄色.其余为白色。求:(1)如果已经从中取定了5个黄球和3个篮球,并将他们编上不同的号码后排成一排,那么使蓝色小球互不相邻的排法有多少种?
(2)如果从袋里取出3个相同颜色彩球(无白色)的概率是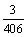 ,且
,且 ,计算红球有几
,计算红球有几
个?
(3)根据(2)得结论,计算从袋中任取3个小球,至少有一个是红球的概率?
15.用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同,且两端的格子的颜色也不同,则不同的涂色方法共有___________种。
14.在某项测量中测量结果 服从正态分布
服从正态分布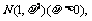 若分在(0.1)内取值的概率为0.4,则分在(0.2)内取值的概率为_____________。
若分在(0.1)内取值的概率为0.4,则分在(0.2)内取值的概率为_____________。
13.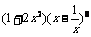 的展开式中常数项为____________。
的展开式中常数项为____________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com