
4.已知函数f(x)=2x的反函数为y=f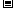 1(x),若f
1(x),若f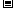 1(a)+f
1(a)+f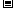 1(b)=3,则a2+b2的最小值为(
)
1(b)=3,则a2+b2的最小值为(
)
A.12 B.18 C.16
D.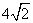
3.若函数f(x)=2sin( )对任意x都有
)对任意x都有 ,则f(
,则f( )等于 ( )
)等于 ( )
A.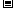 2或2 B.2或0 C.0 D.
2或2 B.2或0 C.0 D.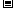 2或0
2或0
2.直线ax+2y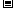 1=0与x+(a
1=0与x+(a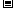 1)y+2=0平行,则a等于
( )
1)y+2=0平行,则a等于
( )
A. B.2 C.
B.2 C.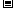 1
D.2或
1
D.2或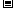 1
1
1.条件P:x∈A∪B,则 P是
( )
P是
( )
A.x A或x
A或x B
B.x
B
B.x A且x
A且x B
B
C.x∈A∩B
D.x A或x∈B
A或x∈B
22.已知函数f(x)(x∈R)满足下列条件:对任意的实数x1、x2都有 ≤
≤ [f(x1)
[f(x1)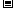 f(x2)]和|f(x1)
f(x2)]和|f(x1)
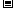 f(x2)|≤|x1-x2|,其中
f(x2)|≤|x1-x2|,其中 是大于0的常数,设实数a0,a,b满足f(a0)=0,b=a
是大于0的常数,设实数a0,a,b满足f(a0)=0,b=a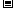
 f(a).
f(a).
(1)证明 ≤1,并且不存在b0≠a0,使得f(b0)=0
≤1,并且不存在b0≠a0,使得f(b0)=0
(2)证明(b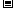 a0)2≤(1
a0)2≤(1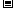
 2)(a
2)(a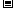 a0)2
a0)2
(3)证明[f(b)]2≤(1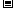
 ) [f(a)]2
) [f(a)]2
21.设数列{an}的前n项和为Sn,已知a1=1,a2=6,a3=11,且(5n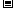 8)Sn+1
8)Sn+1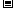 (5n+2)Sn=An+B,n=1,2,3,…,其中A、B为常数.
(5n+2)Sn=An+B,n=1,2,3,…,其中A、B为常数.
(1)求A与B的值.
(2)证明数列{an}为等差数列.
20.设函数f(x)= (a∈R).
(a∈R).
(1)当a=1时,求满足f(x)>2的x的集合
(2)求a的取值范围,使f(x)在区间(0,+ )上是单调递增函数
)上是单调递增函数
19.已知一曲线是与两个定点O(0,0),A(3,0)的距离之比为 的点的轨迹.
的点的轨迹.
(1)求此曲线C的方程
(2)设P(x,y)为曲线C上任意一点,求 的取值范围
的取值范围
18.已知 ,若f(x)=
,若f(x)= ·
· +1,求:
+1,求:
(1)f(x)的表达式及周期
(2)y=lg[f(x)]的单调递增区间
17.已知n次多项式Pn(x)=a0xn+
a1xn-1+…+an-1x+an,如果在一种算法中,计算x0k(k=2,3,4,…,n)的值需要k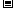 1次乘法,计算P3(x0)的值需要9次运算(6次乘法,3次加法),那么计算Pn(x0)的值共需要
次运算。
1次乘法,计算P3(x0)的值需要9次运算(6次乘法,3次加法),那么计算Pn(x0)的值共需要
次运算。
下面结出一种减少运算次数的算法:P0(x)=a0 ,PK+1(x)=xPk(x)+ak+1(k=0,1,2…,n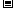 1),利用该算法,计算P3(x0)的值共需要6次运算,计算Pn(x0)的值共需要 次运算。
1),利用该算法,计算P3(x0)的值共需要6次运算,计算Pn(x0)的值共需要 次运算。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com