
5.已知实数x,y满足条件,则z=2x+y的最大值为_ _.
4.函数f (x)=|sinx+cosx|的周期是_ _.
3.函数f(x)=的单调递减区间是_ _.
2.若(a-2i )i=b-i,其中a、b∈R,i是虚数单位,则a2+b2=_ _.
1.已知集合M={x||x-1|≤2,x∈R},P={x|x2-4x-5>0,x∈R },则M∩P=_ _.
20.(本小题满分13分)已知抛物线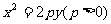 ,过焦点F的动直线
,过焦点F的动直线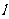 交抛物线于A,B 两点,抛物线在A,B两点处的切线相交于点Q.
交抛物线于A,B 两点,抛物线在A,B两点处的切线相交于点Q.
(1)求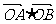 的值;
的值;
(2)求点Q的纵坐标;
(3)证明: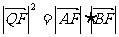 .
.
19.(本小题满分14分)已知数列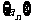 的前
的前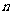 项和为
项和为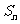 ,
,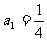 ,且
,且
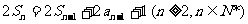 .数列
.数列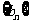 满足
满足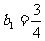 , 且
, 且
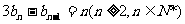 .
.
(1)求证:数列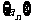 为等差数列;
为等差数列;
(2)求证:数列 为等比数列;
为等比数列;
(3)求数列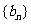 的通项公式以及前
的通项公式以及前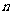 项和
项和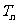 .
.
18.(本小题满分13分)有甲、乙、丙、丁四名网球运动员,通过对过去战绩的统计,在一场比赛中,甲对乙、丙、丁取胜的概率分别为0.6,0.8,0.9.
(1)若甲和乙之间进行三场比赛,求甲恰好胜两场的概率;
(2)若四名运动员每两人之间进行一场比赛,求甲恰好胜两场的概率.
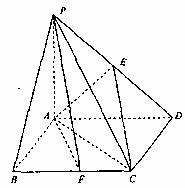
17.(本小题满分14分)如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,
PB⊥BC,PD⊥CD,且PA=2,E为PD中点。
(1)求证:PA⊥平面ABCD;
(2)求二面角E-AC-D的大小;
(3)若F为线段BC的中点,求点D到平面PAF的距离.
16.(本小题满分13分)已知函数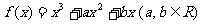 的图象过点
的图象过点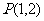 ,且在点
,且在点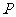 处的切线斜率为8.
处的切线斜率为8.
(1)求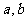 的值;
的值;
(2)求函数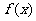 的单调区间;
的单调区间;
(3)求函数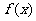 在区间
在区间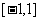 的最值.
的最值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com