
4.在航天员进行的一项太空实验中,要先后实施6个程序,其中程序A只能出现在第一步,程序B和C实施时必须相邻,请问实验顺序的编排方法共有 ( )
A.24种 B.36种 C.48种 D.96种
3.设等差数列{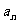 }的前n项和为
}的前n项和为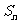 ,
,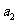 、
、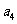 是方程
是方程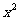 -x-2=0的两个根,则
-x-2=0的两个根,则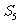 = ( )
= ( )
A.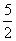 B.5 C.
B.5 C. 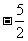 D.-5
D.-5
2.函数y=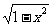 (-1≤x≤0)的反函数是
( )
(-1≤x≤0)的反函数是
( )
A.y=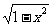 (-1≤x≤0) B.y=-
(-1≤x≤0) B.y=-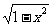 (0≤x≤1)
(0≤x≤1)
C.y=-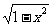 (-1≤x≤0) D.y=
(-1≤x≤0) D.y=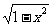 (0≤x≤1)
(0≤x≤1)
1.设集合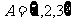 ,则集合A的子集的个数是
( )
,则集合A的子集的个数是
( )
A.3个 B. 6个 C. 7个 D.8个
20.(本小题满分14分)已知函数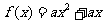 和
和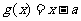 .其中
.其中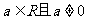 .
.
(Ⅰ)若函数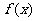 与
与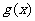 的图像的一个公共点恰好在x轴上,求
的图像的一个公共点恰好在x轴上,求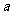 的值;
的值;
(Ⅱ)若函数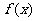 与
与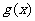 图像相交于不同的两点A、B,O为坐标原点,试问:△OAB的面积S有没有最值?如果有,求出最值及所对应的
图像相交于不同的两点A、B,O为坐标原点,试问:△OAB的面积S有没有最值?如果有,求出最值及所对应的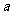 的值;如果没有,请说明理由.
的值;如果没有,请说明理由.
(Ⅲ)若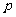 和
和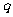 是方程
是方程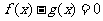 的两根,且满足
的两根,且满足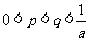 ,证明:当
,证明:当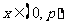 时,
时,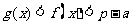 .
.
19.(本小题满分14分)数列 中,
中,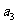 =1,
=1,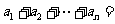
 (n=1,2,3…).
(n=1,2,3…).
(Ⅰ)求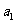 ,
,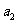 ;
;
(Ⅱ)求数列 的前n项和
的前n项和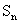 ;
;
(Ⅲ)设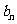 =log2
=log2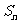 ,存在数列{
,存在数列{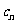 }使得
}使得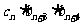 = 1+ n(n+1)(n+2)
= 1+ n(n+1)(n+2)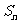 ,试求数列{
,试求数列{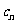 }的前n项和.
}的前n项和.
18.(本小题满分13分)已知椭圆的中心在坐标原点,离心率为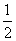 ,一个焦点是F(0,1).
,一个焦点是F(0,1).
(Ⅰ)求椭圆方程;
(Ⅱ)直线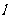 过点F交椭圆于A、B两点,且点F分向量
过点F交椭圆于A、B两点,且点F分向量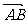 所成的比为2,求直线
所成的比为2,求直线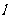 的方程.
的方程.
17.(本小题满分13分)在某次趣味运动会中,甲、乙、丙三名选手进行单循环赛(即每两人比赛一场),共赛三场,每场比赛胜者得1分,输者得0分,没有平局;在每一场比赛中,甲胜乙的概率为 ,甲胜丙的概率为
,甲胜丙的概率为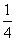 ,乙胜丙的概率为
,乙胜丙的概率为 .
.
(Ⅰ)求甲获得小组第一且丙获得小组第二的概率;
(Ⅱ)求三人得分相同的概率;
(Ⅲ)设在该小组比赛中甲得分数为ξ,求Eξ.
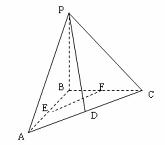
16.(本小题满分14分)如图:在三棱锥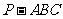 中,
中,
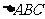 是直角三角形,
是直角三角形,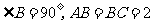 ,
,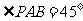 ,点
,点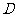 、
、 分别为
分别为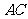 、
、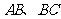 的中点.
的中点.
(Ⅰ)求证: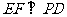 ;
;
(Ⅱ)求直线 与平面
与平面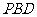 所成的角的大小;
所成的角的大小;
(Ⅲ)求二面角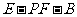 的正切值.
的正切值.
15.(本小题满分12分)记关于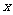 的不等式
的不等式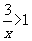 (
(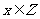 )的解集为A,关于
)的解集为A,关于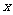 的方程
的方程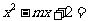 0的解集为B,且
0的解集为B,且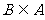 .
.
(Ⅰ)求集合A;
(Ⅱ)求实数m的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com