

4.已知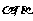 、
、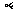 是三个互不重合的平面,
是三个互不重合的平面,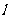 是一条直线,给出下列四个命题:
是一条直线,给出下列四个命题:
①若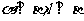 ,则
,则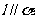 ; ②若
; ②若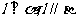 ,则
,则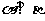 ;
;
③若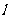 上有两个点到
上有两个点到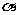 的距离相等,则
的距离相等,则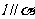 ;
;
④若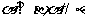 ,则
,则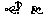 .
.
其中正确命题的序号是 ( )
A.①② B.①④ C.②④ D.③④
3.“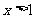 ”是“
”是“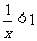 ”成立的 ( )
”成立的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.已知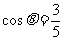 ,且
,且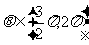 ,则
,则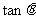 的值为 ( )
的值为 ( )
A.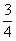 B.
B.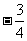 C.
C.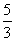 D.
D.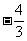
1.i是虚数单位,复数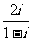 等于 ( )
等于 ( )
A.1+i B.1-i C.-1+i D.-1-i
20.(本小题满分14分)已知函数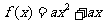 和
和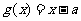 .其中
.其中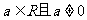 .
.
(Ⅰ)若函数 与
与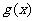 的图像的一个公共点恰好在x轴上,求
的图像的一个公共点恰好在x轴上,求 的值;
的值;
(Ⅱ)若函数 与
与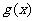 图像相交于不同的两点A、B,O为坐标原点,试问:△OAB的面积S有没有最值?如果有,求出最值及所对应的
图像相交于不同的两点A、B,O为坐标原点,试问:△OAB的面积S有没有最值?如果有,求出最值及所对应的 的值;如果没有,请说明理由.
的值;如果没有,请说明理由.
(Ⅲ)若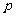 和
和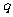 是方程
是方程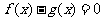 的两根,且满足
的两根,且满足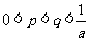 ,证明:当
,证明:当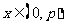 时,
时,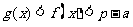 .
.
19.(本小题满分14分)数列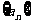 中,
中,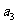 =1,
=1,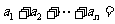
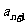 (n=1,2,3…).
(n=1,2,3…).
(Ⅰ)求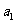 ,
,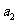 ;
;
(Ⅱ)求数列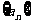 的前n项和
的前n项和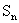 ;
;
(Ⅲ)设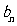 =log2
=log2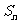 ,存在数列{
,存在数列{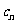 }使得
}使得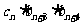 = 1,试求数列{
= 1,试求数列{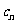 }的前n项和.
}的前n项和.
18.(本小题满分13分)已知椭圆的中心在原点,离心率为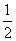 ,一个焦点是F(0,1).
,一个焦点是F(0,1).
(Ⅰ)求椭圆方程;
(Ⅱ)直线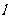 过点F交椭圆于A、B两点,且点F分向量
过点F交椭圆于A、B两点,且点F分向量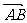 的比为2,求直线
的比为2,求直线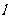 的斜率.
的斜率.
17.(本小题满分13分)在某次趣味运动会中,甲、乙、丙三名选手进行单循环赛(即每两人比赛一场),共赛三场,每场比赛胜者得1分,输者得0分,没有平局;在每一场比赛中,甲胜乙的概率为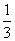 ,甲胜丙的概率为
,甲胜丙的概率为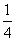 ,乙胜丙的概率为
,乙胜丙的概率为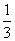 .
.
(Ⅰ)求甲获得小组第一且丙获得小组第二的概率;
(Ⅱ)求三人得分相同的概率;
(Ⅲ)求甲不是小组第一的概率.
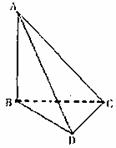
16.(本小题满分14分)在如图所示的四面体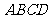 中,
中,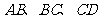 两两互相垂直,且
两两互相垂直,且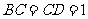 .
.
(Ⅰ)求证:平面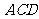
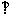 平面
平面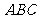 ;
;
(Ⅱ)求二面角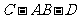 的大小;
的大小;
(Ⅲ)若直线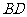 与平面
与平面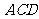 所成的角为
所成的角为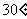 ,求线段
,求线段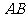 的长度.
的长度.
15.(本小题满分12分)记关于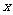 的不等式
的不等式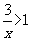 (
(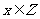 )的解集为A,关于
)的解集为A,关于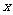 的方程
的方程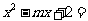 0的解集为B,且
0的解集为B,且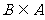 .
.
(Ⅰ)求集合A;
(Ⅱ)求实数m的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com