
3.函数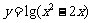 的定义域是____________________.
的定义域是____________________.
2.已知复数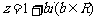 ,z2是纯虚数,则
,z2是纯虚数,则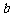 的值是______________.
的值是______________.
1.设集合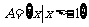 ,
,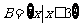 ,则
,则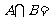 _______________.
_______________.
21.(本小题满分12分)在直角坐标平面上有一点列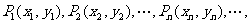 对一切正整数n,点Pn在函数
对一切正整数n,点Pn在函数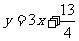 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以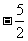 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}.
(1)求点Pn的坐标;
(2)设抛物线列C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,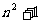 ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求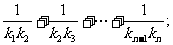
(3)设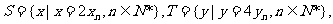 等差数列
等差数列 的任一项
的任一项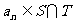 ,其中
,其中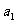 是
是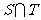 中的最大数,
中的最大数,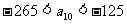 ,求数列
,求数列 的通项公式.
的通项公式.
20.(本小题满分12分)某投资商到一开发区投资72万元建起一座蔬菜加工厂,第一年共支出12万元,以后每年支出增加4万元,从第一年起每年蔬菜销售收入50万元.设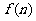 表示前n年的纯利润总和(f(n)=前n年的总收入一前n年的总支出一投资额).
表示前n年的纯利润总和(f(n)=前n年的总收入一前n年的总支出一投资额).
(1)该厂从第几年开始盈利?
(2)若干年后,投资商为开发新项目,对该厂有两种处理方案:①年平均纯利润达到最大时,以48万元出售该厂;②纯利润总和达到最大时,以16万元出售该厂,问哪种方案更合算?
19.(本小题满分12分)已知定点A(-2,0),动点B是圆F: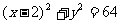 (F为圆心)上一点,线段AB的垂直平分线交BF于P.
(F为圆心)上一点,线段AB的垂直平分线交BF于P.
(1)求动点P的轨迹E的方程;
(2)直线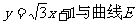 交于M,N两点,试问在曲线E位于第二象限部分上是否存在一点C,使
交于M,N两点,试问在曲线E位于第二象限部分上是否存在一点C,使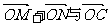 共线(O为坐标原点)?若存在,求出点C的坐标;若不存在,请说明理由.
共线(O为坐标原点)?若存在,求出点C的坐标;若不存在,请说明理由.
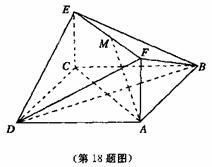
18.(本小题满分10分)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=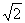 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
(1)求证:AM//平面BDE;
(2)求二面角A-DF-B的大小.
17.(本小题满分10分)已知函数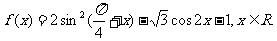
(1)求函数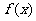 的最小正周期;
的最小正周期;
(2)若对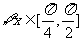 ,不等式
,不等式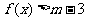 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
16.定义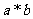 是向量a和b的“向量积”,它的长度
是向量a和b的“向量积”,它的长度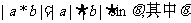 为向量a和b的夹角,若
为向量a和b的夹角,若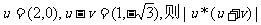 =
.
=
.
15.定义在R上的奇函数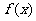 满足:对于任意
满足:对于任意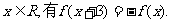
若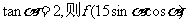 的值为
.
的值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com