3．如图：计算机执行下面程序段后，输出的结果为

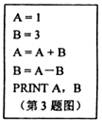
A．1，3　　　　　　　　　　　 B．4，－2 　　　　　　　 C．4，1 　　　　　　　　　　 D．0，0

2．已知角a满足sin2a<0，cosa－sina<0，则角a在

A．第一象限　　 　　　　 B．第二象限　　 　　　　 C．第三象限　　 　　　　 D．第四象限

1．频率分布直方图中最高小矩形的中间位置所对的数字特征是

A．中位数　　 　　　　　　 B．众数　　 　　　　　　　　 C．平均数　　 　　　　　　 D．标准差

22．(本小题满分14分)

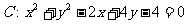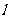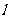　　　 已知圆，问是否存在斜率为1的直线，使以被圆C截得的弦AB为直径的圆经过原点。若存在，写出直线的方程；若不存在，说明理由。

21．(本小题满分12分)

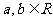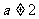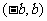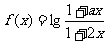　　　 设，且，定义在区间内的函数是奇函数。

①求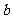的取值范围；

②判断并用定义证明函数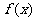的单调性。

20．(本小题满分12分)

　　　 我国加入WTO时，根据达成的协议，若干年内某产品关税与市场供应量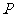的关系允许近似满足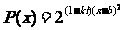，其中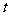为关税税率，且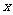，为市场价格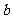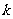，、为正常数，当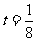时，市场供应量如图所示。

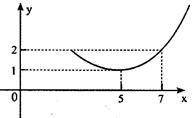
①根据图像求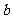、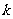的值；

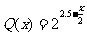②记市场需求量为，它近似满足，当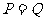时的市场价格为市场平衡价格，为使市场平衡价格不低于9元，求税率的最大值。

19．(本小题满分l2分)　　

已知：正四棱锥S-ABCD的棱长均为13，E、F分别是SA、BD上的点，且SE∶EA=BF∶FD=5∶8。

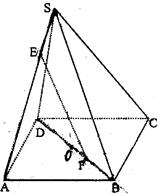
①求证：直线EF∥平面SBC；

②求四棱锥S-ABCD的体积。

18．(本小题满分12分)

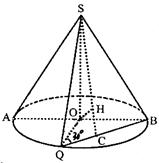
如图所示，圆锥的轴截面为等腰直角△SAB，Q为底面圆周上一点。

①若QB的中点为C，OH⊥SC，求证OH⊥平面SBQ；

②如果∠AOQ=60°，QB=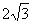，求此圆锥的全面积。

17．(本小题满分12分)

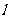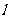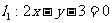已知两点A(4, 4)、B(6, 3)到直线的距离相等，且过两直线和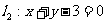的交点，求直线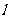的方程。

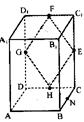
16．如下图：正四棱柱ABCD-A₁B₁C₁D₁中，E、F、G、H分别是棱C₁C、C₁D，、D₁D、DC的中点，点M在四边形EFGH上及其内部运动，则M只须满足条件　　　　　　 时，就有MN∥平面B₁BDD₁(N是BC的中点)。(填上正确的一个条件即可，不必考虑全部可能情况)