

5.三点(3,l0),(7,20),(11,24)的回归方程是( )
A.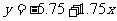 B.
B.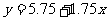
C.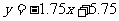 D.
D.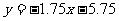
4.若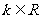 ,则“
,则“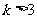 ”是“方程
”是“方程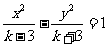 表示双曲线”的( )
表示双曲线”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.命题“所有被5整除的整数都是奇数”的否定是( )
A.所有被5整除的整数都不是奇数 B.所有奇数都不能被5整除
C.存在一个被5整除的整数不是奇数 D.存在一个奇数,不能被5整除
2.将一个长与宽不等的长方形,沿对角线分成四个区域,如图涂上四种颜色,中间装个指针,使其可以自由转动,对指针停留的可能性下列说法正确的是( )
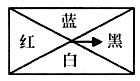
A.一样大 B.蓝白区域大
C.红黑区域大 D.由指针转动圈数定
1.将两个数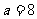 ,
,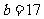 交换,使
交换,使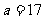 ,
,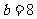 ,下面语句正确的一组是( )
,下面语句正确的一组是( )
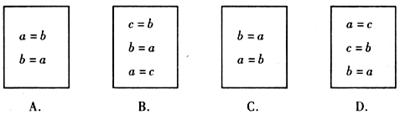
(17)(本小题满分12分)
有以下真命题:设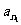 ,
,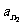 ,……
,……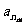 是公差为
是公差为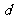 的等差数列
的等差数列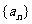 中的任意m项,
中的任意m项,
若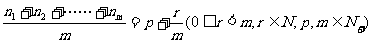 ①,
①,
则有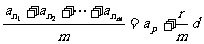 ②;
②;
特别地,当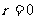 时,称
时,称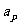 是
是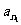 ,
,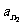 ,……
,……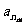 的等差平均项。
的等差平均项。
(I)当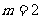 ,
,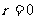 时,试写出与上述命题中的①、②两式相对应的等式;
时,试写出与上述命题中的①、②两式相对应的等式;
(Ⅱ)已知等差数列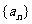 中,
中,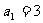 ,
,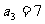 ,
,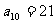 ,
,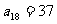 ,试根据上述命题求
,试根据上述命题求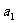 ,
,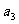 ,
,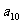 ,
,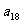 的等差平均项;
的等差平均项;
(III)试将上述真命题推广到各项为正实数的等比数列中,写出相应的命题。
(18)(本小题满分12分)
某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
|
|
积极参加班级工作 |
不太主动参加班级工作 |
合计 |
|
学习积极性高 |
18 |
7 |
25 |
|
学习积极性一般 |
6 |
19 |
25 |
|
合计 |
24 |
26 |
50 |
(I)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(Ⅱ)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由。(参考下表)
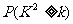 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
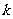 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(19)(本小题满分12分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量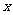 (吨)与相应的生产能耗
(吨)与相应的生产能耗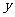 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
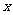 |
3 |
4 |
5 |
6 |
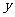 |
2.5 |
3 |
4 |
4.5 |
(I)请在给出的坐标系内,画出上表数据的散点图。
(Ⅱ)请根据上表提供的数据,用最小二乘法求出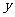 关于
关于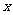 的线性回归方程
的线性回归方程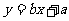 ;
;
(Ⅲ)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(II)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(20)(本小题满分12分)
对于任意实数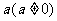 和
和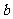 ,不等式
,不等式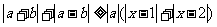 恒成立,求实数
恒成立,求实数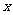 的取值范围。
的取值范围。
(21)(本小题满分12分)
一般轮船在航行中的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料赞是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每公里的费用总和最小?
(22)(本小题满分14分)
设函数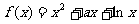 。
。
(I)当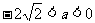 时,判断函数
时,判断函数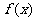 在定义域上的单调性;
在定义域上的单调性;
(II)求函数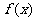 的极值点。
的极值点。
(13)设函数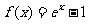 的图像与
的图像与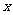 轴相交于点P,则曲线在点P处的切线方程是
。
轴相交于点P,则曲线在点P处的切线方程是
。
(14)在极坐标系中,若过点(4,0)且与极轴垂直的直线交曲线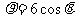 于A,B两点,则
于A,B两点,则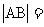 。
。
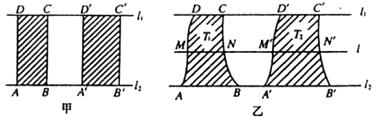
(15)如图甲,矩形ABCD和矩形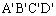 夹在两条平行线l1、l2之间,且
夹在两条平行线l1、l2之间,且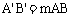 ,则容易得到矩形ABCD的面积S1与矩形
,则容易得到矩形ABCD的面积S1与矩形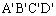 的面积S2满足:S2=mS1。由此类比,如图乙,夹在两平行线、l2之间的两个封闭图形T1、T2,如果任意作一条与l1平行的直线l,l分别与两个图形T1、T2的边界交于M、N、
的面积S2满足:S2=mS1。由此类比,如图乙,夹在两平行线、l2之间的两个封闭图形T1、T2,如果任意作一条与l1平行的直线l,l分别与两个图形T1、T2的边界交于M、N、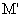 、
、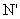 ,且
,且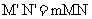 ,则T1、T2的面积S1、S2满足S2=mS1。椭圆
,则T1、T2的面积S1、S2满足S2=mS1。椭圆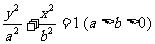 与圆
与圆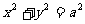 是夹在直线
是夹在直线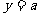 与
与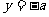 之间的封闭图形,类比上面的结论,由圆的面积可得椭圆的面积为
。
之间的封闭图形,类比上面的结论,由圆的面积可得椭圆的面积为
。
(16)两个分类变量X、Y,它们的值域分别是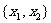 、
、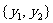 ,其样本频数列联表为
,其样本频数列联表为
|
|
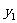 |
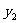 |
总计 |
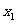 |
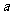 |
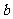 |
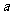 + +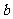 |
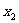 |
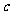 |
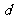 |
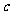 + +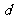 |
|
总计 |
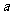 + +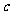 |
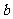 + +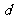 |
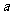 + +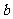 + +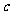 + +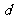 |
若两个分类变量X、Y独立,则下列结论
①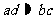 ;②
;②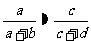 ;③
;③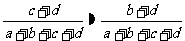 ;
;
④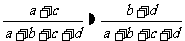 ;⑤
;⑤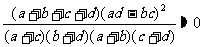 中,
中,
正确的命题序号是 。(将正确命题序号都填上)
(1)复数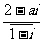 (
(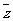 是z的共轭复数,a∈R)是纯虚数,则a=
是z的共轭复数,a∈R)是纯虚数,则a=
(A)0 (B)1 (C)2 (D)3
(2)下面框图属于
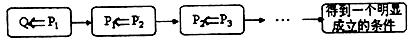
(A)流程图 (B)结构图 (C)程序框图 (D)工序流程图
(3)设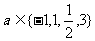 ,则使函数
,则使函数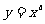 的定义域为R且为奇函数的所有
的定义域为R且为奇函数的所有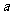 值为
值为
(A)1,3 (B)-1,1 (C)-l,3 (D)-1,1,3
(4)二次函数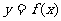 的图象过原点,且它的导函数
的图象过原点,且它的导函数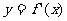 的图象如图所示,则
的图象如图所示,则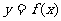 的图象是
的图象是
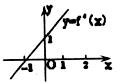
(A)关于直线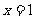 对称的抛物线 (B)关于直线
对称的抛物线 (B)关于直线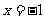 对称的抛物线
对称的抛物线
(C)顶点在第二象限的抛物线 (D)顶点在第四象限的抛物线
(5)如图,圆O的割线PBA过圆心O,弦CD交PA于点F, 且△COF∽△PDF,PB=OA=2,则PF=
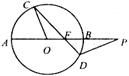
(A)2 (B)3 (C)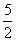 (D)
(D)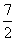
(6)已知曲线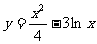 的一条切线的斜率为
的一条切线的斜率为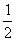 ,则切点的横坐标为
,则切点的横坐标为
(A)3 (B)2 (C)1 (D)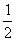
(7)参数方程为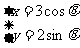 (
(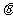 为参数)的曲线上的点M到直线
为参数)的曲线上的点M到直线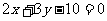 的距离最小,则M点的坐标
的距离最小,则M点的坐标
(A)(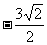 ,
,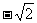 ) (B)(
) (B)(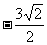 ,
,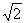 )
)
(C)(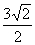 ,
,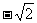 ) (D)(
) (D)(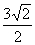 ,
,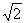 )
)
(8)有两种花色的正六边形地面砖,按下图的规律拼成若干个图案,则第6个图案中有菱形纹的正六边形的个数是

(A)26 (B)31 (C)32 (D)36
(9)设函数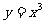 与
与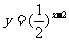 的图像的交点为
的图像的交点为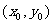 ,则
,则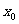 所在的区间是
所在的区间是
(A)(0,1) (B)(1,2) (C)(2,3) (D)(3,4)
(10)若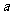 ,
,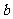 为非零实数,则下列四个命题都成立:
为非零实数,则下列四个命题都成立:
①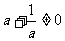 ; ②
; ②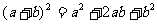 ;
;
③若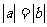 ,则
,则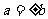 ; ④若
; ④若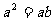 ,则
,则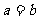 ,则对于任意非零复数
,则对于任意非零复数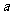 、
、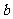 ,上述命题仍然成立的序号是
,上述命题仍然成立的序号是
(A)①② (B)②④ (C)③④ (D)①③
(11)函数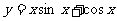 在下面哪个区间内是增函数
在下面哪个区间内是增函数
(A)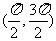 (B)
(B)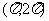 (C)
(C)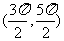 (D)
(D)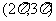
(12)函数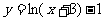 的图像恒过定点A,若点A在直线上
的图像恒过定点A,若点A在直线上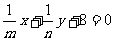 上,其中
上,其中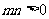 ,则
,则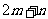 的最小值为
的最小值为
(A)1 (B)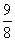 (C)
(C)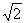 (D)
(D)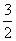
第Ⅱ卷(共90分)
(17)(本小题满分12分)
有以下真命题:设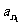 ,
,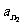 ,……
,……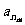 是公差为
是公差为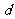 的等差数列
的等差数列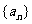 中的任意m项,
中的任意m项,
若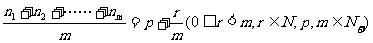 ①,
①,
则有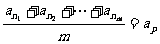 ②;
②;
特别地,当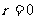 时,称
时,称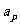 ,是
,是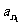 ,
,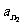 ,……
,……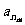 的等差平均项。
的等差平均项。
(I)当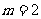 ,
,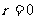 时,试写出与上述命题中的①、②两式相对应的等式;
时,试写出与上述命题中的①、②两式相对应的等式;
(Ⅱ)已知等差数列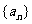 中,
中,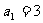 ,
,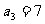 ,
,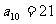 ,
,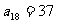 ,试根据上述命题求
,试根据上述命题求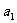 ,
,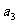 ,
,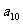 ,
,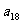 的等差平均项;
的等差平均项;
(III)试将上述真命题推广到各项为正实数的等比数列中,写出相应的命题。
(18)(本小题满分12分)
某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
|
|
积极参加班级工作 |
不太主动参加班级工作 |
合计 |
|
学习积极性高 |
18 |
7 |
25 |
|
学习积极性一般 |
6 |
19 |
25 |
|
合计 |
24 |
26 |
50 |
(I)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(Ⅱ)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由。(参考下表)
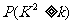 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
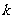 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(19)(本小题满分12分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量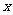 (吨)与相应的生产能耗
(吨)与相应的生产能耗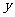 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
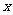 |
3 |
4 |
5 |
6 |
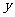 |
2.5 |
3 |
4 |
4.5 |
(I)请在给出的坐标系内,画出上表数据的散点图。
(Ⅱ)请根据上表提供的数据,用最小二乘法求出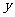 关于
关于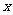 的线性回归方程
的线性回归方程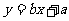 ;
;
(Ⅲ)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(II)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(20)(本小题满分12分)
对于任意实数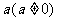 和
和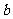 ,不等式
,不等式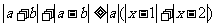 恒成立,求实数
恒成立,求实数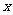 的取值范围。
的取值范围。
(21)(本小题满分12分)
某高等学校自愿献血的50位同学的血型分布情形如下表:
|
血型 |
A |
B |
AB |
0 |
|
人数 |
20 |
10 |
5 |
15 |
(I)今从这50人中随机选出两人,问两人血型相同的概率是多少?
(Ⅱ)今有A血型的病人需要输血,从血型为A、O的同学中随机选出2人准备献血,记选出A血型的人数为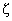 ,求随机变量
,求随机变量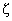 的分布列及数学期望E
的分布列及数学期望E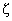 。
。
(22)(本小题满分14分)
设函数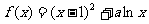 。
。
(I)当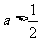 时,判断函数
时,判断函数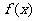 在定义域上的单调性;
在定义域上的单调性;
(II)求函数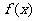 的极值点。
的极值点。
(13)已知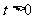 ,若
,若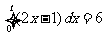 ,则
,则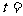 。
。
(14)在极坐标系中,若过点(4,0)且与极轴垂直的直线交曲线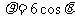 于A,B两点,则
于A,B两点,则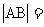 。
。
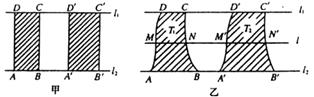
(15)如图甲,矩形ABCD和矩形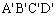 夹在两条平行线l1、l2之间,且
夹在两条平行线l1、l2之间,且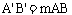 ,则容易得到矩形ABCD的面积S1与矩形
,则容易得到矩形ABCD的面积S1与矩形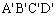 的面积S2满足:S2=mS1。由此类比,如图乙,夹在两平行线、l2之间的两个封闭图形T1、T2,如果任意作一条与l1平行的直线l,l分别与两个图形T1、T2的边界交于M、N、
的面积S2满足:S2=mS1。由此类比,如图乙,夹在两平行线、l2之间的两个封闭图形T1、T2,如果任意作一条与l1平行的直线l,l分别与两个图形T1、T2的边界交于M、N、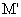 、
、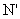 ,且
,且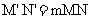 ,则T1、T2的面积S1、S2满足S2=mS1。椭圆
,则T1、T2的面积S1、S2满足S2=mS1。椭圆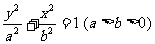 与圆
与圆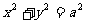 是夹在直线
是夹在直线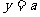 与
与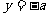 之间的封闭图形,类比上面的结论,由圆的面积可得椭圆的面积为
。
之间的封闭图形,类比上面的结论,由圆的面积可得椭圆的面积为
。
(16)两个分类变量X、Y,它们的值域分别是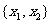 、
、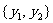 ,其样本频数列联表为
,其样本频数列联表为
|
|
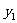 |
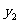 |
总计 |
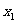 |
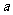 |
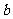 |
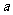 + +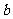 |
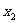 |
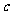 |
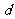 |
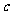 + +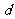 |
|
总计 |
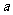 + +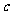 |
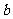 + +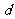 |
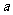 + +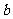 + +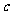 + +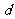 |
若两个分类变量X、Y独立,则下列结论
①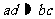 ;②
;②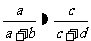 ;③
;③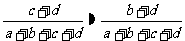 ;
;
④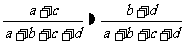 ;⑤
;⑤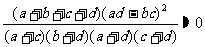 中,
中,
正确的命题序号是 。(将正确命题序号都填上)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com